题目内容
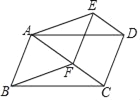
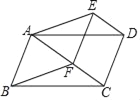
【题目】如图，平行四边形ABCD，F是对角线AC上的一点，过点D作DE∥AC，且DE＝CF，连接AE、DE、EF．
（1）求证：△ADE≌△BCF；
（2）若∠BAF+∠AED＝180°，求证：四边形ABFE为菱形．
【答案】（1）见解析；（2）见解析.
【解析】
（1）根据平行四边形的性质和全等三角形的判定证明即可；
（2）根据平行四边形的判定和菱形的判定解答即可．
（1）∵平行四边形ABCD，∴AD＝BC，AD∥BC，∴∠DAC＝∠BCF．
∵DE∥AC，∴∠DAC＝∠EDA，∴∠FCB＝∠EDA．
在△ADE与△BCF中，∵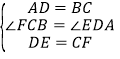
，∴△ADE≌△BCF（SAS）；
（2）∵DE∥AC，且DE＝AC，∴四边形EFCD是平行四边形，∴DC＝EF，且DC∥EF．
又∵AB＝CD，AB∥CD，∴AB＝EF，AB∥EF，∴四边形ABFE是平行四边形．
∵△ADE≌△BCF，∴∠AED＝∠BFC．
∵∠BAF+∠AED＝180°，∴∠BAF+∠BFC＝180°．
又∵∠BFA+∠BFC＝180°，∴∠BAF＝∠BFA，∴BA＝BF，∴四边形ABFE为菱形．
练习册系列答案
相关题目
【题目】在平面直角坐标系xOy中，抛物线C1：y＝﹣x2+2x．
（1）补全表格：
抛物线 | 顶点坐标 | 与x轴交点坐标 | 与y轴交点坐标 | |
y＝﹣x2+2x | （1，1） |
|
| （0，0） |
（2）将抛物线C1向上平移3个单位得到抛物线C2，请画出抛物线C1，C2，并直接回答：抛物线C2与x轴的两交点之间的距离是抛物线C1与x轴的两交点之间距离的多少倍．
