题目内容
【题目】如图1,水坝的横截面是梯形ABCD,∠ABC=37°,坝顶DC=3m,背水坡AD的坡度i(即tan∠DAB)为1:0.5,坝底AB=14m.
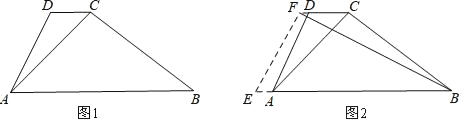
(1)求坝高;
(2)如图2,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底间时拓宽加固,使得AE=2DF,EF⊥BF,求DF的长.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
【答案】(1)6m;(2)(2![]() ﹣7)m
﹣7)m
【解析】(1)作DM⊥AB于M,CN⊥AN于N.由题意:tan∠DAB=![]() =2,设AM=x,则DM=2x,在Rt△BCN中,求出BN,构建方程即可解决问题;
=2,设AM=x,则DM=2x,在Rt△BCN中,求出BN,构建方程即可解决问题;
(2)作FH⊥AB于H.设DF=y,则AE=2y,EH=3+2y-y=3+y,BH=14+2y-(3+y)=11+y,由△EFH∽△FBH,可得![]() ,即
,即![]() ,求出y即可;
,求出y即可;
(1)作DM⊥AB于M,CN⊥AB于N.
由题意:tan∠DAB=![]() =2,设AM=x,则DM=2x,
=2,设AM=x,则DM=2x,
∵四边形DMNC是矩形,
∴DM=CN=2x,
在Rt△NBC中,tan37°=![]() ,
,
∴BN=![]() x,
x,
∵x+3+![]() x=14,
x=14,
∴x=3,
∴DM=6,
答:坝高为6m.
(2)作FH⊥AB于H.设DF=y,则AE=2y,EH=3+2y-y=3+y,BH=14+2y-(3+y)=11+y,
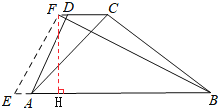
由△EFH∽△FBH,可得![]() ,
,
即![]() ,
,
解得y=-7+2![]() 或-7-2
或-7-2![]() (舍弃),
(舍弃),
∴DF=2![]() -7,
-7,
答:DF的长为(2![]() -7)m.
-7)m.

练习册系列答案
相关题目