题目内容
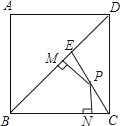
【题目】如图,边长为1的正方形ABCD中,点E是对角线BD上的一点,且BE=BC,点P在EC上,PM⊥BD于M,PN⊥BC于N,则PM+PN=_____.
【答案】![]()
【解析】
连接BP作EF⊥BC于点F,由正方形的性质可知△BEF为等腰直角三角形,根据边长为1,得到BE=1,可求EF,利用面积法得S△BPE+S△BPC=S△BEC,将面积公式代入即可.
解:连接BP作EF⊥BC于点F则∠EFB=90°,由正方形的性质可知∠EBF=45°,
∴△BEF为等腰直角三角形,
又根据正方形的边长为1,得到BE=BC=1,
在直角三角形BEF中,sin∠EBF=![]() ,即,BF=EF=BEsin45°=1×
,即,BF=EF=BEsin45°=1×![]() ,
,
又PM⊥BD,PN⊥BC,
∴S△BPE+S△BPC=S△BEC,即![]() BE×PM+
BE×PM+![]() ×BC×PN=
×BC×PN=![]() ,
,
∵BE=BC,
PM+PN=EF=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目