��Ŀ����
����Ŀ����֪����ʽ![]() �ǹ���
�ǹ���![]() �Ķ��ζ���ʽ��
�Ķ��ζ���ʽ��
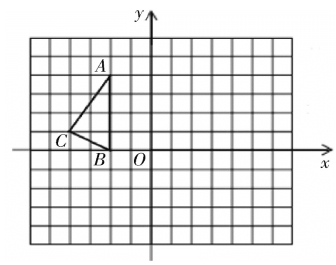
��1������գ�![]() ______��
______��![]() ______��
______��![]() ______��
______��
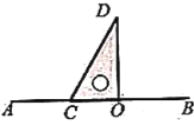
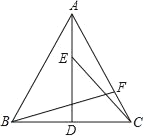
��2����ͼ����![]() ��
��![]() �������߶�
�������߶�![]() �ϣ���
�ϣ���![]() ��
��![]() ��
��![]() ����ֱ����߶�
����ֱ����߶�![]() ��
��![]() ���е㣬��
���е㣬��![]() �����߶�
�����߶�![]() �ij���
�ij���
![]()
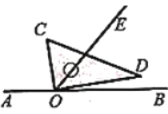
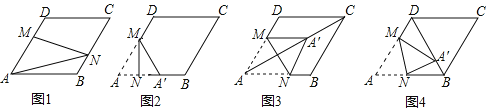
��3����ͼ����![]() ��
��![]() ��
��![]() �ֱ���������
�ֱ���������![]() ��
��![]() ��
��![]() �����ʾ������
�����ʾ������![]() ����
����![]() �㵽ԭ��ľ�����ȣ���λ��ԭ�����࣬����������
�㵽ԭ��ľ�����ȣ���λ��ԭ�����࣬����������![]() ��
��![]() ��������ͬʱ��ʼ�˶������е�
��������ͬʱ��ʼ�˶������е�![]() ����2����λÿ����ٶȴ�
����2����λÿ����ٶȴ�![]() ���˶���
���˶���![]() �㣬����5����λÿ����ٶ��˶���
�㣬����5����λÿ����ٶ��˶���![]() �㣬�����8����λÿ����ٶȷ��ص�
�㣬�����8����λÿ����ٶȷ��ص�![]() ��ֹͣ�˶���������
��ֹͣ�˶���������![]() ����2����λÿ����ٶȴ�
����2����λÿ����ٶȴ�![]() ���˶���
���˶���![]() �㣬����12����λÿ����ٶȷ��ص�
�㣬����12����λÿ����ٶȷ��ص�![]() ��ֹͣ�˶����ڴ��˶������У�
��ֹͣ�˶����ڴ��˶������У�![]() ��
��![]() ���㵽
���㵽![]() ��ľ����Ƿ����ȣ�����ȣ���ֱ��д����ʱ��
��ľ����Ƿ����ȣ�����ȣ���ֱ��д����ʱ��![]() �������ϱ�ʾ������������ȣ���˵�����ɣ�
�������ϱ�ʾ������������ȣ���˵�����ɣ�
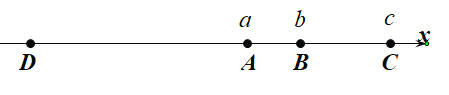
���𰸡���1��2��4��8����2��28����3������ȣ���ʱ��![]() �������ϱ�ʾ������4��
�������ϱ�ʾ������4��![]() ��
��![]() ��
��![]() ��
��
��������
��1�����ö���ʽ�Ķ��壬�ó�x�Ĵ�����ϵ�������ó��𰸣�
��2������![]() �Լ���1���Ľ�����EG��GH��HF�ij��������߶εĺͲ��ʾ��MN����MN=10���ɵó��𰸣�
�Լ���1���Ľ�����EG��GH��HF�ij��������߶εĺͲ��ʾ��MN����MN=10���ɵó��𰸣�
��3����t���![]() ��
��![]() ���㵽
���㵽![]() ��ľ�����ȣ��ֱ���t��ʾ��AQ��AP���������̽�����⣮
��ľ�����ȣ��ֱ���t��ʾ��AQ��AP���������̽�����⣮
�⣺��1���߶���ʽ![]() �ǹ���
�ǹ���![]() �Ķ��ζ���ʽ��
�Ķ��ζ���ʽ��
��a-2=0��![]() =2��b+4��0��c-8=0��
=2��b+4��0��c-8=0��
��a=2��b=4��c=8��
��2����![]() ��a=2��b=4��c=8��
��a=2��b=4��c=8��

��EG=2x��GH=4x��HF=8x��
��EF=14x��EH=6x��GF=12x��
��![]() ��
��![]() ����ֱ����߶�
����ֱ����߶�![]() ��
��![]() ���е㣬
���е㣬
��MH=3x��NF=6x��HN=HF-NF=2x��
��MN=MH+HN=5x=10��
��x=2��
��EF=14x=14��2=28��
��3����t���![]() ��
��![]() ���㵽
���㵽![]() ��ľ�����ȣ�
��ľ�����ȣ�

��![]() ��
��![]() ��
��![]() �ֱ���������
�ֱ���������![]() ��
��![]() ��
��![]() �����ʾ������
�����ʾ������![]() ����
����![]() �㵽ԭ��ľ�����ȣ���λ��ԭ�����࣬a=2��b=4��c=8��
�㵽ԭ��ľ�����ȣ���λ��ԭ�����࣬a=2��b=4��c=8��
��D���ʾ������-8��
��AD=10��AB=2��BC=4��AC=6��
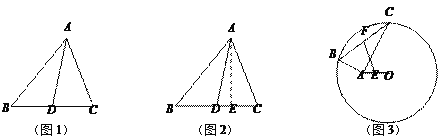
��0<t��3ʱ����ͼ1��
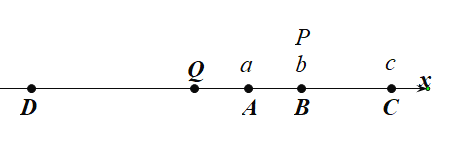
������ã� PC=BQ=2t��AP=AQ��
��AC-PC=BQ-AB��
��6-2t=2t-2��
��ã�t=2��
���![]() �������ϱ�ʾ������8-PC=8-2t=4��
�������ϱ�ʾ������8-PC=8-2t=4��
��3<t��5ʱ����ͼ2��
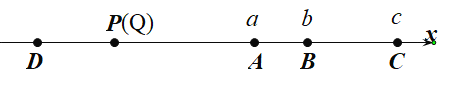
������ã�AP=AQ��BQ=2t��AP=5(t-3)��
��AP=BQ-AB����5(t-3)= 2t-2��
��ã�t=![]() ��
��
��AP=2t-2=![]() ��
��
���![]() �������ϱ�ʾ������
�������ϱ�ʾ������![]() =
=![]() ��
��
��5<t��6ʱ����ͼ3��

������ã�AP=AQ��BQ=2t��DP= 8(t-5)��DQ=12-2t��
��8(t-5)= 12-2 t��
��ã�t=![]() ��
��
��BQ =2t=![]() ��
��
���![]() �������ϱ�ʾ������
�������ϱ�ʾ������![]() =
=![]() ��
��
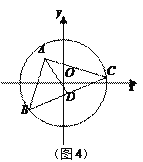
��6<t��5ʱ����ͼ4��
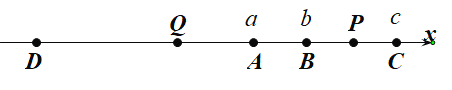
������ã�AP=AQ��AQ=10-12(t-6)��DP=8(t-5)��
��AP=DP-AD����10-12(t-6)= 8(t-5)-10��
��ã�t=![]() ��
��
��AP= 8(t-5)-10=![]() ��
��
���![]() �������ϱ�ʾ������
�������ϱ�ʾ������![]() =
=![]() ��
��
��![]() ��
��![]() ���㵽
���㵽![]() ��ľ������ʱ��
��ľ������ʱ��![]() �������ϱ�ʾ������4��
�������ϱ�ʾ������4��![]() ��
��![]() ��
��![]() ��
��

 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�