题目内容
【题目】阅读下面材料,完成(1)~(2)题:
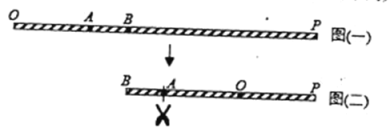
数学课上,老师出示了一道题:如图1,将一个直角三角板![]() 的直角边
的直角边![]() 摆放在直线
摆放在直线![]() 上,然后以直角顶点
上,然后以直角顶点![]() 为旋转中心顺时针旋转这个三角板.若射线
为旋转中心顺时针旋转这个三角板.若射线![]() 平分
平分![]() 、探究
、探究![]() 和
和![]() 的数量关系,并说明经过一段时间的思考后,同学们开始了交流:
的数量关系,并说明经过一段时间的思考后,同学们开始了交流:
小明:我根据老师的叙述画出图2,并计算出当![]() 时,
时,![]() 的度数是
的度数是![]() ;
;
小红:在小明的图形中,点![]() 、
、![]() 都在
都在![]() 的上方,我发现,在这种情况下,
的上方,我发现,在这种情况下,![]() 始终在
始终在![]() 的内部.若设
的内部.若设![]() 的度数是
的度数是![]() ,通过计算,
,通过计算,![]() 的度数可以用含
的度数可以用含![]() 的式子表示,得到
的式子表示,得到![]() 和
和![]() 的数量关系是
的数量关系是![]() ;
;
小华:我除了画小明的这种图形,还画了其余几种,也分别得出![]() 和
和![]() 的数量关系,从而解决了老师提出的问题.
的数量关系,从而解决了老师提出的问题.
老师:这些同学都先画出图形,再解决问题,这体现了图形的直性,但要注意一点,在初中阶段我们研究的角都是小于![]() 的.随着大家交流的深入,点
的.随着大家交流的深入,点![]() 的位置由
的位置由![]() 上方到直线
上方到直线![]() 外,
外,![]() 的值由数字到字母,这体现了从特殊到一般的思想,同学们再根据小华所说的进行探究,还能归纳出其他的数学思想方法!
的值由数字到字母,这体现了从特殊到一般的思想,同学们再根据小华所说的进行探究,还能归纳出其他的数学思想方法!
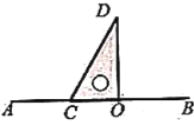
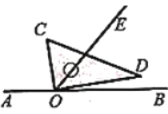
图1 图2
(1)如图2,点![]() 、
、![]() 都在
都在![]() 上方,
上方,![]() .
.
①用含![]() 的代数式表示
的代数式表示![]() 为_____________;
为_____________;
②小红的“![]() 始终在
始终在![]() 的内部”的说法是正确的吗,为什么?
的内部”的说法是正确的吗,为什么?
(2)根据小华的叙述,写出![]() 与
与![]() 的数量关系并说明.
的数量关系并说明.
【答案】(1)①![]() ;②
;②![]() 始终在
始终在![]() 的内部; (2)当点
的内部; (2)当点![]() 在
在![]() 的上方,点
的上方,点![]() 在
在![]() 的下方的图形时,
的下方的图形时, ![]()
![]() ;当点
;当点![]() 在
在![]() 的下方,点
的下方,点![]() 在
在![]() 的上方时,
的上方时, ![]()
![]() ;当点
;当点![]() 、
、![]() 都在
都在![]() 的下方时,
的下方时, ![]()
![]() .
.
【解析】
(1)①观察图形,寻找角之间的关系,可以发现![]() .
.
②小红说法是正确的,只要证明当点![]() 、
、![]() 都在
都在![]() 的上方时,
的上方时, ![]() 即可.
即可.
(2)继续旋转三角尺,分别作出点![]() 在
在![]() 的上方,点
的上方,点![]() 在
在![]() 的下方的图形; 点
的下方的图形; 点![]() 在
在![]() 的下方,点
的下方,点![]() 在
在![]() 的上方的图形; 点
的上方的图形; 点![]() 、
、![]() 都在
都在![]() 的下方的图形并一一解答即可.
的下方的图形并一一解答即可.
解: (1)①观察图形可得![]() .
.
②当点![]() 、
、![]() 都在
都在![]() 的上方时,
的上方时, ![]()
因为![]() ,
,
所以![]() ,
,
所以![]() 始终在
始终在![]() 的内部.
的内部.
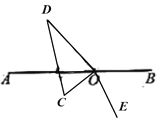
(2)第一种情况,当点![]() 在
在![]() 的上方,点
的上方,点![]() 在
在![]() 的下方的图形时,如图:
的下方的图形时,如图:
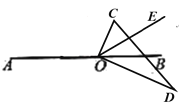
此时![]()
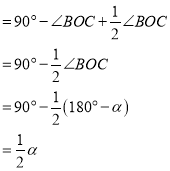
第二种情况,当点![]() 在
在![]() 的下方,点
的下方,点![]() 在
在![]() 的上方时,如下图:
的上方时,如下图:
此时![]()
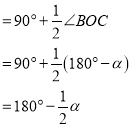
第三种情况,当点![]() 、
、![]() 都在
都在![]() 的下方时,如下图:
的下方时,如下图:
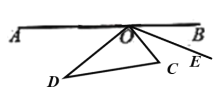
此时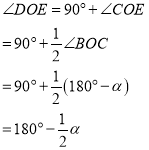

 阅读快车系列答案
阅读快车系列答案