题目内容
【题目】(1)探究:
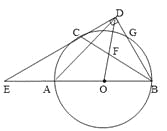
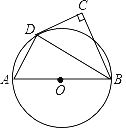
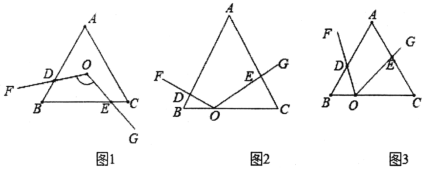
问题:如图1,等边三角形ABC的边长为6,点O是∠ABC和∠ACB的角平分线交点,∠FOG=120°,绕点O任意旋转∠FOG,分别交△ABC的两边于D,E两点求四边形ODBE的面积.
讨论:
①甲:在∠FOG旋转过程中,当OF经过点B时,OG一定经过点C.
②乙:小明的分析有道理,这样,我们就可以利用“ASA”证出△ODB≌△OEC.
③丙:因为△ODB≌△OEC,所以只要算出△OBC的面积就得出了四边形ODBE的面积.
老师:同学们的思路很清晰,也很正确,在分析和解决问题时,我们经常会借用特例作辅助线来解决一般问题请你按照探究的思路,直接写出四边形ODBE的面积:________.
(2)应用:
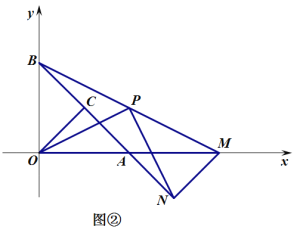
①特例:如图2,∠FOG的顶点O在等边三角形ABC的边BC上,OB=2,OC=4,边OG⊥AC于点E,OF⊥AB于点D,求△BOD面积.
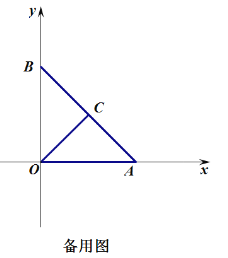
②探究:如图3,已知∠FOG=60°,顶点O在等边三角形ABC的边BC上,OB=2,OC=4,记△BOD的面积为x,△COE的面积为y,求xy的值.
【答案】探究:3![]() ;应用:①
;应用:①![]() ;②12.
;②12.
【解析】
(1)(1)由“ASA”可证△DOB≌△EOC,可得S△DOB=S△EOC,可得S△OBC=四边形ODBE的面积,即可求解;
(2)①由直角三角形的性质可求OD,BD的长,即可求解;
②过点O作OM⊥AB于M,ON⊥AC于N,可求OM=![]() ,ON=2
,ON=2![]() ,通过证明△BDO∽△COE,可得
,通过证明△BDO∽△COE,可得![]() =
=![]() ,可得BDEC=OBOC=8,即可求解;
,可得BDEC=OBOC=8,即可求解;
解:(1)方法引导:
如图1,连接OB,OC,
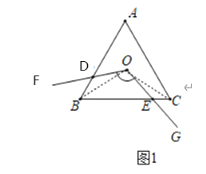
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵点O是∠ABC和∠ACB的角平分线交点,
∴∠ABO=∠OBC=∠OCB=30°,
∴OB=OC,∠BOC=∠FOG=120°,
∴∠DOB=∠COE,且OB=OC,∠ABO=∠BCO,
∴△DOB≌△EOC(ASA)
∴S△DOB=S△EOC,
∴S△OBC=四边形ODBE的面积,
∵等边三角形ABC的边长为6,
∴S△ABC=![]() ×62=9
×62=9![]() ,
,
∴S△OBC=四边形ODBE的面积=![]() S△ABC=3
S△ABC=3![]() ,
,
故答案为:3![]() ;
;
(2)①∵△ABC是等边三角形,∠B=60°,
∵OF⊥AB,
∴∠BOD=30°,
∵OB=2,
∴BD=1,
∴OD=![]() ,
,
∴△BOD的面积=![]() ×1×
×1×![]() =
=![]() ;
;
②过点O作OM⊥AB于M,ON⊥AC于N,
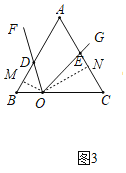
由①得:OM=![]() ,同理:ON=2
,同理:ON=2![]() ,
,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠DOC=∠B+∠BDO=∠DOG+∠COG,且∠FOG=60°,
∴∠COG=∠BDO,且∠B=∠C=60°,
∴△BDO∽△COE,
∴![]() =
=![]() ,
,
∴BDEC=OBOC=8,
∴xy=![]() ×BD×
×BD×![]() ×
×![]() ×CE×2
×CE×2![]() =12;
=12;

 名校课堂系列答案
名校课堂系列答案【题目】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:
组别 | 个数段 | 频数 | 频率 |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
(1)表中的数![]() ,
,![]() ;
;
(2)估算该九年级排球垫球测试结果小于10的人数;
(3)排球垫球测试结果小于10的为不达标,若不达标的5人中有3个男生,2个女生,现从这5人中随机选出2人调查,试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率.