题目内容
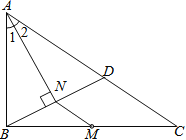
【题目】如图,在△ABC中,O是AC上一动点(不与点A、C重合),过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)OE与OF相等吗?证明你的结论;
(2)试确定点O的位置,使四边形AECF是矩形,并加以证明.

【答案】(1)OE=OF(2)当O运动到AC中点时,四边形AECF是矩形
【解析】整体分析:
(1)利用等角对等边分别判断OE=OC,OF=OC;(2)先判断四边形AECF是平行四边形,再证明∠ECF=90°.
解:(1)OE=OF,
∵MN∥BC,
∴∠OEC=∠BCE,∠OFC=∠FCD,
∵CE平分∠ACB,CF平分∠ACD,
∴∠BCE=∠ACE,∠OCF=∠FCD,
∴∠ACE=∠OEC,∠OCF=∠OFC,
∴OE=OC,OC=OF,
∴OE=OF.
(2)当O运动到AC中点时,四边形AECF是矩形,
∵AO=CO,OE=OF,
∴四边形AECF是平行四边形,
∵∠ECA+∠ACF=![]() ∠BCD,
∠BCD,
∴∠ECF=90°,
∴四边形AECF是矩形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某采摘农场计划种植A,B两种草莓共6亩,根据表格信息,解答下列问题:
项目 品种 | A | B |
年亩产(单位:千克) | 1200 | 2000 |
采摘价格 | 60 | 40 |
(1)若该农场每年草莓全部被采摘的总收入为460000元,那么A、B两种草莓各种多少亩?
(2)若要求种植A种草莓的亩数不少于种植B种草莓的一半,那么种植A种草莓多少亩时,可使该农场每年草莓全部被采摘的总收入最多?并求出最多总收入.