题目内容
【题目】如图∠1=∠2,CF⊥AB,DE⊥AB,求证:FG∥BC.
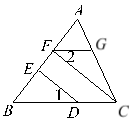
证明:∵CF⊥AB,DE⊥AB (已知)
∴∠BED=90°,∠BFC=90°( )
∴∠BED=∠BFC ( )
∴ED∥FC ( )
∴∠1=∠BCF ( )
∵∠2=∠1 ( 已知 )
∴∠2=∠BCF ( )
∴FG∥BC ( )
【答案】垂直定义;等量代换;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行
【解析】
试题根据垂直的定义及平行线的判定和性质依次分析即可.
∵CF⊥AB ,DE⊥AB (已知)
∴∠BED=90° ,∠BFC=90°( 垂直定义 )
∴∠BED=∠BFC ( 等量代换 )
∴ED∥FC ( 同位角相等,两直线平行 )
∴∠1=∠BCF ( 两直线平行,同位角相等 )
∵∠2=∠1 ( 已知 )
∴∠2=∠BCF ( 等量代换 )
∴FG∥BC ( 内错角相等,两直线平行 )

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】2018年3月,某市教育主管部门在初中生中开展了“文明礼仪知识竞赛”活动,活动结束后,随机抽取了部分同学的成绩(x均为整数,总分100分),绘制了如下尚不完整的统计图表.
调查结果统计表
组别 | 成绩分组(单位:分) | 频数 | 频率 |
A | 80≤x<85 | 50 | 0.1 |
B | 85≤x<90 | 75 | |
C | 90≤x<95 | 150 | c |
D | 95≤x≤100 | a | |
合计 | b | 1 |
根据以上信息解答下列问题:
(1)统计表中,a=_____,b=_____,c=_____;
(2)扇形统计图中,m的值为_____,“C”所对应的圆心角的度数是_____;
(3)若参加本次竞赛的同学共有5000人,请你估计成绩在95分及以上的学生大约有多少人?