题目内容
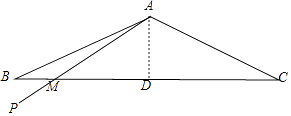
【题目】在△ABC中,AB=AC,∠BAC=150°,点A到BC的距离为1,与AB重合的一条射线AP,从AB开始,以每秒15°的速度绕点A逆时针匀速旋转,到达AC后立即以相同的速度返回AB,到达后立即重复上述旋转过程,设AP与BC边的交点为M,旋转2019秒时,BM= , CM= . 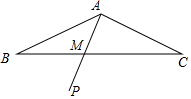
【答案】2;2+2 ![]()
【解析】解:过A作AD⊥BC于D,则AD=1, ∵150=10×15,即AP从AB开始,绕点A逆时针匀速旋转10秒到达AC后再经过10秒返回AB,
而2019=100×20+19=100×20+10+9,
∴当旋转2019秒时,AP从AB绕点A逆时针匀速旋转了9秒,
∴此时CAP=15°×9=135°,
∴∠BAP=150°﹣135°=15°,
∵AB=AC,
∴BD=CD,∠B=∠C= ![]() (180°﹣150°)=15°,
(180°﹣150°)=15°,
∴AM=BM,∠AMD=∠B+∠BAP=30°,
∴BM=AM=2AD=2,MD= ![]() ,
,
∴CD=BD=2+ ![]() ,
,
∴CM=2+2 ![]() ,
,
所以答案是:2,2+2 ![]() .
.
【考点精析】掌握等腰三角形的性质和旋转的性质是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角);①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

 阅读快车系列答案
阅读快车系列答案【题目】如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E. 
(1)求证:DE是⊙O的切线;
(2)如果AD=5,AE=4,求AC长.
【题目】2018年3月,某市教育主管部门在初中生中开展了“文明礼仪知识竞赛”活动,活动结束后,随机抽取了部分同学的成绩(x均为整数,总分100分),绘制了如下尚不完整的统计图表.
调查结果统计表
组别 | 成绩分组(单位:分) | 频数 | 频率 |
A | 80≤x<85 | 50 | 0.1 |
B | 85≤x<90 | 75 | |
C | 90≤x<95 | 150 | c |
D | 95≤x≤100 | a | |
合计 | b | 1 |
根据以上信息解答下列问题:
(1)统计表中,a=_____,b=_____,c=_____;
(2)扇形统计图中,m的值为_____,“C”所对应的圆心角的度数是_____;
(3)若参加本次竞赛的同学共有5000人,请你估计成绩在95分及以上的学生大约有多少人?

【题目】某超市销售进价为2元的雪糕,在销售中发现,此商品的日销售单价x(元)与日销售量y(根)之间有如下关系:
日销售单价x(元) | 3 | 4 | 5 | 6 |
日销售量y(根) | 40 | 30 | 24 | 20 |
(1)猜测并确定y和x之间的函数关系式;
(2)设此商品销售利润为W,求W与x的函数关系式,若物价局规定此商品最高限价为10元/根,你是否能求出商品日销售最大利润?若能请求出,不能请说明理由.