题目内容
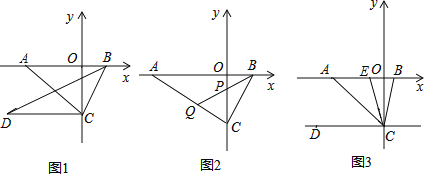
【题目】如图1,在平面直角坐标系中,点A为x轴负半轴上一点,点B为x轴正半轴上一点,![]() ,
,![]() ,其中a、b满足关系式:
,其中a、b满足关系式:![]() .
.
![]() ______,
______,![]() ______,
______,![]() 的面积为______;
的面积为______;
![]() 如图2,石
如图2,石![]() 于点C,点P是线段OC上一点,连接BP,延长BP交AC于点
于点C,点P是线段OC上一点,连接BP,延长BP交AC于点![]() 当
当![]() 时,求证:BP平分
时,求证:BP平分![]() ;
;![]() 提示:三角形三个内角和等于
提示:三角形三个内角和等于![]()
![]() 如图3,若
如图3,若![]() ,点E是点A与点B之间上一点连接CE,且CB平分
,点E是点A与点B之间上一点连接CE,且CB平分![]() 问
问![]() 与
与![]() 有什么数量关系?请写出它们之间的数量关系并请说明理由.
有什么数量关系?请写出它们之间的数量关系并请说明理由.
【答案】(1)![]() ;
;![]() ;6;(2)证明见解析;(3)
;6;(2)证明见解析;(3)![]() ,理由见解析.
,理由见解析.
【解析】
(1)求出CD的长度,再根据三角形的面积公式列式计算即可得解;
(2)根据等角的余角相等解答即可;
(3)首先证明∠ACD=∠ACE,推出∠DCE=2∠ACD,再证明∠ACD=∠BCO,∠BEC=∠DCE=2∠ACD即可解决问题;
【解答】(1)解:如图1中,
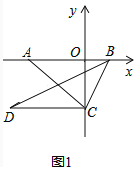
∵|a+4|+(b-a-1)2=0,
∴a=-4,b=-3,
∵点C(0,-4),D(-3,-4),
∴CD=3,且CD∥x轴,
∴△BCD的面积=![]() ×4×3=6;
×4×3=6;
故答案为-4,-3,6.
(2)如图2中,
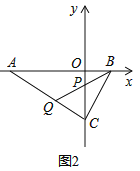
∵∠CPQ=∠CQP=∠OPB,AC⊥BC,
∴∠CBQ+∠CQP=90°,
又∵∠ABQ+∠CPQ=90°,
∴∠ABQ=∠CBQ,
∴BQ平分∠CBA.
(3)如图3中,结论:∠BEC=2∠BCO.
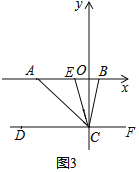
理由:∵AC⊥BC,
∴∠ACB=90°,
∴∠ACD+∠BCF=90°,
∵CB平分∠ECF,
∴∠ECB=∠BCF,
∴∠ACD+∠ECB=90°,
∵∠ACE+∠ECB=90°,
∴∠ACD=∠ACE,
∴∠DCE=2∠ACD,
∵∠ACD+∠ACO=90°,∠BCO+∠ACO=90°,
∴∠ACD=∠BCO,
∵C(0,-4),D(-3,-4),
∴CD∥AB,
∠BEC=∠DCE=2∠ACD,
∴∠BEC=2∠BCO,