Question

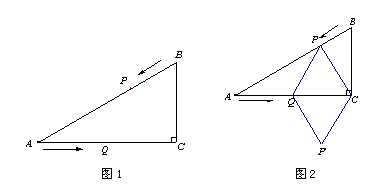
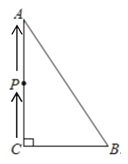
【题目】如图，△ABC中，，，，若点P从点C出发，以每秒1cm的速度沿折线C→A→B→C运动(回到C点后点P停止运动)，设运动时间为t秒()．

（1）若点P点AB边上，且满足时，求出此时t的值；

（2）若点P恰好在∠BAC的角平分线上，求出此时t的值；

（3）在运动过程中，当△BCP为等腰三角形时，直接写出所有满足条件的t的值．

Answer 1

【答案】（1）6.5s；（2）s；（3）6.5s或6s或5.4s或3s．

【解析】

（1）根据题意，，，，可得AC=4cm，当P点在AB边上，且满足时，则t=4+计算即可；

（2）当点P恰好在∠BAC的角平分线上时，做PD⊥AB于D，则PD=CP，利用三角形面积，代入数据计算即可得；

（3）当△BCP为等腰三角形时，分情况讨论：①当CP=BP时；②当CB=BP时；③当CP=CB时，分别计算即可．

（1）∵，，，

∴根据勾股数可知AC=4cm，

∵P点在AB边上，且满足时，

∴PA=AB=cm，

又∵点P的速度是每秒1cm，

∴t=4+=6.5（s）；

故答案为：6.5s；

（2）过点P作PD⊥AB于D，如图所示，

∵点P恰好在∠BAC的角平分线上，

∴PD=PC，

又t=3+4+5-CP，

由，可得

×3×4=×4×CP+×5×PD，

∴CP=，

∴t=3+4+5-=（s），

故答案为：s；

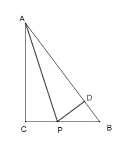
（3）当△BCP为等腰三角形时，

①当CP=BP时，点P在BC的垂直平分线上，作PD⊥BC于D，如下图所示：

∴点D是BC的中点，PD是△ABC的中位线，

∴点P是AB的中点，AP=BP=AB=2.5cm，

∴t=6.5s；

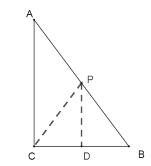
②当CB=BP时，点P在AB上，如下图所示：

∴BP=CB=3cm，

∴t=4+5-3=6（s），

故答案为：6s；

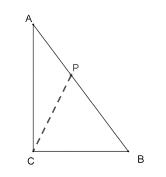
③CP=CB时，如下图所示：

点P在AB上，或者点在AC上两种情况，

若CP=CB时，过点C作CE⊥AB于E，

由等面积法求得CE=2.4cm，

在Rt△BEC中，由勾股定理得，

BE=1.8cm，BP=2BE=3.6cm，

∴t=4+5-3.6=5.4（s），

若C=CB时，则t=C=3s，

故答案为：5.4s或3s；

综上所述，当△BCP为等腰三角形时，满足条件的t值为：6.5或6s或5.4s或3s；

故答案为：6.5s或6s或5.4s或3s．