题目内容
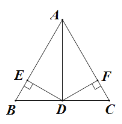
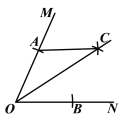
【题目】如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A,B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC.若OA=5,AB=6,则点B到AC的距离为( )
A. 5 B. ![]() C. 4 D.
C. 4 D. ![]()
【答案】B
【解析】
根据题意,作出合适的辅助线,然后根据角平分线的性质、等腰三角形的性质和勾股定理可以求得点B到AC的距离,本题得以解决.
由题意可得,
OC为∠MAN的角平分线,
∵OA=OB,OC平分∠AOB,
∴OC⊥AB,
设OC与AB交于点D,作BE⊥AC于点E,
∵AB=6,OA=5,AC=OA,OC⊥AB,
∴AC=5,∠ADC=90°,AD=3,
∴CD=4,
∵![]() ,
,
∴![]() ,
,
解得,BE=![]() ,
,
故选:B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目