��Ŀ����
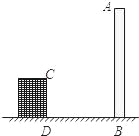
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=3��BC=4������D�ӵ�A������ÿ��3����λ���ٶ��˶�����B������D��DE��AB������AC�ڵ�E�����D���˶�ʱ��Ϊt�루t��0����
��1���߶�AE�ij�Ϊ �� ���ú�t�Ĵ���ʽ��ʾ��
��2������ADE���ACB�������Ϊ1��4ʱ����t��ֵ��
��3�����ADE���ACB�ص�����ͼ�ε��ܳ�ΪL����L��t֮��ĺ�����ϵʽ��
��4����ֱ��DE�ѡ�ACB�ֳɵ�������ͼ������һ������Գ�ͼ��ʱ��ֱ��д��t��ֵ��
���𰸡�
��1��5t
��2��
�⣺����һ����ED��AB��
���ADE=90�㣮�ߡ�ACB=90�㣬
���ACB=��ADE����A=��A��
���ABC�ס�AED��
�� ![]() ��
��
��AD=3t��AC=3��BC=4��
��DE=4t��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ���ᣩ
���ᣩ
��t��ֵΪ ![]() ��
��
����������ED��AB��
���ADE=90�㣮
�ߡ�ACB=90�㣬
���ACB=��ADE��
�ߡ�A=��A��
���ABC�ס�AED��
�� ![]() ��
��
�� ![]() ��
��
��AC=3��AD=3t��
��2��3t=3��t= ![]()
��3��
�⣺�ɣ�2���ã���ABC�ס�AED��
�� ![]() ��
��
��AD=3t��
��DE=4t��AE=5t��BD=5��3t��
�൱ ![]() ʱ��L=3t+4t+5t=12t��
ʱ��L=3t+4t+5t=12t��
��L=12t��
�� ![]() ʱ����ͼ��
ʱ����ͼ��
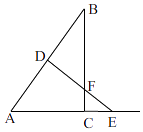
�ߡ�B=��B����BDF=��BCA��
���ABC�ס�FBD��
�� ![]() ��
��
��BD=5��3t��
�� ![]() ��
��
�ߡ�BFD=��EFC����BDF=��ECF��
���B=��E��
�ߡ�FCE=��BCA
���BCA�ס�ECF��
�� ![]() ��
��
��CE=5t��3��
�� ![]() ��
��
![]() ��
��
�� ![]()
��4��
�⣺�ɣ�1��֪��AE=5t��DE=4t��
��CE=3��5t��
��DE=CEʱ���ı���BCED����Գ�ͼ�Σ�
��4t=3��5t��
��t= ![]() ��
��
��DE��BC�ཻ��F��AD=ACʱ���ı���ACFE����Գ�ͼ�Σ�
��AD=3t��AC=3��
��3t=3��
��t=1��
��������������ʱ��tΪ ![]() ��1
��1
���������⣺��1����Rt��ABC�У�tanA= ![]() =
= ![]()
������ã�AD=3t��
��Rt��ADE��tanA= ![]() =
= ![]() =
= ![]() ��
��
���ݹ��ɶ����ã�AE=5t��
���Դ���5t��
�����㾫����������Ŀ����֪���������ù��ɶ����ĸ�������������ε��ж������֪ʶ���Եõ�����Ĵ𰸣���Ҫ����ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2�����������ε��ж�����:���Ƕ�Ӧ��ȣ������������ƣ�ASA����ֱ�������α�б���ϵĸ߷ֳɵ�����ֱ�������κ�ԭ���������ƣ� ���߶�Ӧ�ɱ����Ҽн���ȣ������������ƣ�SAS�������߶�Ӧ�ɱ����������������ƣ�SSS����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�