题目内容
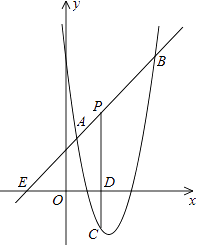
【题目】已知二次函数y=ax2+bx+c的图象与x轴交于(x1 , 0),(x2 , 0)两点,且0<x1<1,1<x2<2,与y轴交于(0,﹣2).下列结论:①2a+b>1; ②a+b>2;③a﹣b<2;④3a+b>0; ⑤a<﹣1.其中正确结论的个数为( )
A.2
B.3
C.4
D.5
【答案】B
【解析】解:如图: 0<x1<1,1<x2<2,并且图象与y轴相交于点(0,﹣2),
可知该抛物线开口向下即a<0,c=﹣2,
①当x=2时,y=4a+2b+c<0,即4a+2b<﹣c;
∵c=﹣2,
∴4a+2b<2,
∴2a+b<1,
故本选项错误;
②∵当x=1时,y>0,
∴a+b+c>0,
∵c=﹣2,
∴a+b﹣2>0,故此选项正确;
③当x=﹣1时,y=a﹣b+c<0,
∵c=﹣2,
∴a﹣b<﹣c,
即a﹣b<2,
故本选项正确;
④∵0<x1<1,1<x2<2,
∴1<x1+x2<3,
又∵x1+x2=﹣ ![]() ,
,
∴1<﹣ ![]() <3,
<3,
∴3a+b<0,
故本选项错误;
⑤∵0<x1x2<2,x1x2= ![]() <2,
<2,
又∵c=﹣2,
∴a<﹣1.
故本选项正确;
故选B.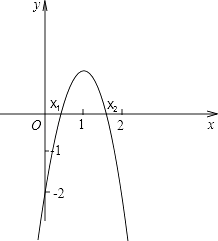
【考点精析】本题主要考查了二次函数图象以及系数a、b、c的关系的相关知识点,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能正确解答此题.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工零件个数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如生产部负责人把每位工人的月加工零件个数定为260,你认为这个定额是否合理?为什么?