题目内容
【题目】已知关于x的方程2x2﹣（4k+2）x+2k2+1=0．
（1）当k取何值时，方程有两个不相等的实数根？
（2）当k取何值时，方程有两个相等的实数根？
（3）当k取何值时，方程没有实数根？
【答案】
（1）解：△=（4k+2）2﹣8（2k2+1）=16k﹣4；
当k＞ 
时，方程有两个不相等的实数根
（2）解：当k= 时，方程有两个相等的实数根
（3）解：当k＜ 时，方程没有实数根
【解析】（1）根据判别式的意义得到△=（4k+2）2﹣8（2k2+1）=16k﹣4＞0，然后解不等式解即可；（2）根据判别式的意义得到△=（4k+2）2﹣8（2k2+1）=16k﹣4=0，求出k的值即可；（3）根据判别式的意义得到△=（4k+2）2﹣8（2k2+1）=16k﹣4＜0，然后解不等式解即可．
【考点精析】通过灵活运用求根公式，掌握根的判别式△=b2-4ac，这里可以分为3种情况：1、当△>0时，一元二次方程有2个不相等的实数根2、当△=0时，一元二次方程有2个相同的实数根3、当△<0时，一元二次方程没有实数根即可以解答此题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
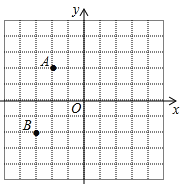
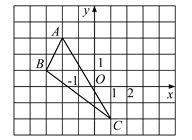
【题目】（1）如图，在平面直角坐标系中，请画出△ABC关于y轴对称的△A′B′C′，并写出A′，B′，C′三点的坐标；（其中A′，B′，C′分别是A，B，C的对应点，不写画法）
（2）求△ABC的面积．
【题目】某乡镇企业生产部有技术工人15人，生产部为了合理制定产品的每月生产定额，统计了这15人某月的加工零件个数：
每人加工零件个数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数．
(2)假如生产部负责人把每位工人的月加工零件个数定为260，你认为这个定额是否合理？为什么？
