题目内容
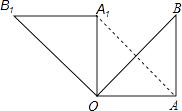
【题目】如图,△ABC,△ADE是等边三角形,B,C,D在同一直线上.
求证:(1)CE=AC+CD;(2)∠ECD=60°.

【答案】证明见解析
【解析】
(1)根据△ABC、△ADE都是等边三角形,得到AE=AD,BC=AC=AB,∠BAC=∠DAE=60°,推出∠BAD=∠CAE,得到△BAD≌△CAE,根据全等三角形的性质得到BD=EC,即可推出答案;
(2)由(1)知:△BAD≌△CAE,根据平角的意义即可求出∠ECD的度数.
(1)∵△ABC,△ADE是等边三角形,
∴AE=AD,BC=AC=AB,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),
∴BD=EC.∵BD=BC+CD=AC+CD,
∴CE=BD=AC+CD.
(2)由(1)知△BAD≌△CAE,
∴∠ACE=∠ABD=60°,
∴∠ECD=180°-∠ACB-∠ACE=60°.

练习册系列答案
相关题目