题目内容
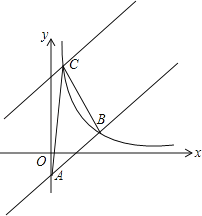
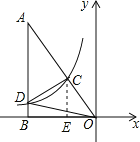
【题目】如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=![]() (x<0)经过斜边OA上的点C,且OC:AC=1:2,与另一直角边交于点D,若S△OCD=12,则k= .
(x<0)经过斜边OA上的点C,且OC:AC=1:2,与另一直角边交于点D,若S△OCD=12,则k= .
【答案】﹣9
【解析】
试题分析:作CE⊥OB于E,如图,根据反比例函数的比例系数k的几何意义得到S△OCE=S△BOD=![]() k,再根据三角形面积公式得到S△ACD=12,且OC=
k,再根据三角形面积公式得到S△ACD=12,且OC=![]() OA,则S△OAB=36+
OA,则S△OAB=36+![]() k,然后证明△OCE∽△OAQB,利用相似三角形的性质即可得到k的值.
k,然后证明△OCE∽△OAQB,利用相似三角形的性质即可得到k的值.
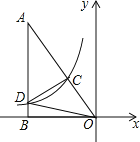
解:作CE⊥OB于E,如图,
∵点C、D在双曲线y=y=![]() (x<0)上,
(x<0)上,
∴S△OCE=S△BOD=![]() k,
k,
∵OC:AC=1:2,S△OCD=12,
∴S△ACD=24,OC=![]() OA,
OA,
∴S△OAB=36+![]() |k|,
|k|,
∵CE∥AB,
∴△OCE∽△OAQB,
∴![]() =(
=(![]() )2,即
)2,即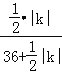 =
=![]() ,
,
∴k=±9.
∵k<0,
∴k=﹣9.
故答案为﹣9.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目