Question

【题目】在矩形ABCD中，AB＝8cm，BC＝6cm，点P从点A出发，沿AB边向点B以每秒2cm的速度移动，同时点Q从点D出发沿DA边向点A以每秒1cm的速度移动，P、Q其中一点到达终点时，另一点随之停止运动．设运动时间为t秒．回答下列问题：

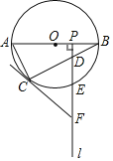
(1)如图①，几秒后△APQ的面积等于5cm2．

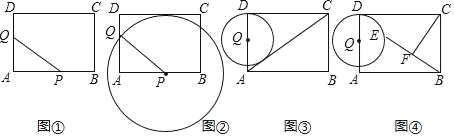
(2)如图②，若以点P为圆心，PQ为半径作⊙P．在运动过程中，是否存在t值，使得点C落在⊙P上？若存在，求出t的值；若不存在，请说明理由．

(3)如图③，若以Q为圆心，DQ为半径作⊙Q，当⊙Q与AC相切时

①求t的值．

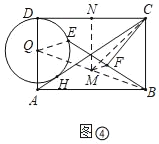
②如图④，若点E是此时⊙Q上一动点，F是BE的中点，请直接写出CF的最小值．

Answer 1

【答案】(1)1秒后△APQ的面积为5；(2)当t＝﹣10+2时，点C落在⊙P上；(3)①；②CF的最小值为．

【解析】

（1）利用三角形的面积公式构建方程即可解决问题．

（2）如图②中，连接PC，根据PQ=PC，利用勾股定理构建方程即可解决问题．

（3）①如图③中，设⊙Q与AC相切于点H，连接QH．在Rt△AQH中，利用勾股定理构建方程即可解决问题．

②如图④中，连接QE，BQ，取BQ的中点M，连接FM，CM，作MN⊥CD于N．求出CM，MF，根据CF≥CM-MF可即可解决问题．

(1)由题意：AP＝2t，DQ＝t．则AQ＝6﹣t．

则×2t(6﹣t)＝5，

整理得t2﹣6t+5＝0，

解得t＝1或5(舍弃)，

∴1秒后△APQ的面积为5．

(2)如图②中，连接PC．

∵⊙P经过点C，

∴PQ＝PC，

∵PA2+AQ2＝PB2+BC2，

∴4t2+(6﹣t)2＝(8﹣2t)2+62，

解得t＝﹣10+2或﹣10﹣2 (舍弃)，

∴当t＝﹣10+2时，点C落在⊙P上．

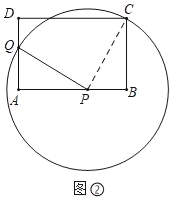
(3)①如图③中，设⊙Q与AC相切于点H，连接QH．

∵CD、CH是圆的切线，

∴CD＝CH＝8，

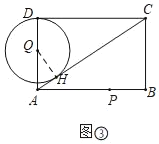
∵QD＝QH＝t，AC＝＝10，

∴AH＝2，

∵QH⊥AC，

∴∠AHQ＝90°，

∴AQ2＝HQ2+AH2，

∴(6﹣t)2＝t2+22，

∴t＝，

∴t＝时，⊙Q与AC相切．

②如图④中，连接QE，BQ，取BQ的中点M，连接FM，CM，作MN⊥CD于N．

∵MQ＝MB，FB＝FE，

∴FMEQ＝DQ＝，

∵AD∥MN∥BC，QM＝MB，

∴DN＝NC＝4，MN＝ (DQ+BC)＝，

∴CM＝＝＝，

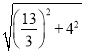∵CF≥CM﹣FN，

∴CF≥，

∴CF的最小值为．