题目内容
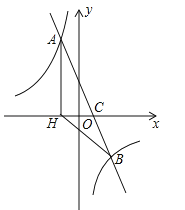
【题目】如图,已知![]() 、
、![]() 两点是直线
两点是直线![]() 与
与![]() 轴的正半轴,
轴的正半轴,![]() 轴的正半轴的交点,如果
轴的正半轴的交点,如果![]() ,
,![]() 的长分别是x2-14x+48=0的两个根
的长分别是x2-14x+48=0的两个根![]() ,射线
,射线![]() 平分
平分![]() 交
交![]() 轴于
轴于![]() 点,
点,
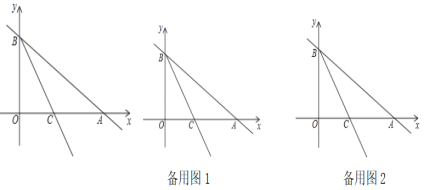
(1)求![]() ,
,![]() 的长.
的长.
(2)求点![]() 的坐标.
的坐标.
(3)在坐标平面内找点![]() ,使
,使![]() ,
,![]() ,
,![]() ,
,![]() 四个点为顶点的四边形是平行四边形?若存在,请直接写出点
四个点为顶点的四边形是平行四边形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() 的长是
的长是![]() ,
,![]() 的长是
的长是![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 的坐标是
的坐标是![]() 、
、![]() 或
或![]() .
.
【解析】
(1)由![]() ,
,![]() 的长分别是x2-14x+48=0的两个根
的长分别是x2-14x+48=0的两个根![]() ,可以解一元二次方程求出
,可以解一元二次方程求出![]() 和
和![]() 的长度.
的长度.
(2)作![]() 垂直
垂直![]() 于
于![]() ,利用角平分线定理并设
,利用角平分线定理并设![]() ,利用
,利用![]() 建立含x的等量关系方程,从而求得C的坐标.
建立含x的等量关系方程,从而求得C的坐标.
(3)首先肯定存在这样的Q点,运用四边形ABCQ为平行四边形时当![]() 、
、![]() 交于点
交于点![]() ,
,![]() 、
、![]() 交于点
交于点![]() ,
,![]() 、
、![]() 交于点
交于点![]() ,分别设点
,分别设点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,从而分析求值.
,从而分析求值.
![]() 由
由![]() ,
,
解得![]() 或
或![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,![]() ,
,
即![]() 的长是
的长是![]() ,
,![]() 的长是
的长是![]() .
.
![]() ∵ 射线
∵ 射线![]() 平分
平分![]() 交
交![]() 轴于
轴于![]() 点,作
点,作![]() 垂直
垂直![]() 于
于![]() ,如图所示:
,如图所示:
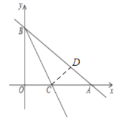
根据角平分线性质得,![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
解得![]() ,即
,即![]() .
.
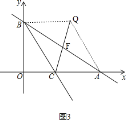
![]() 如图
如图![]() ,
,![]() 、
、![]() 交于点
交于点![]() ,
,
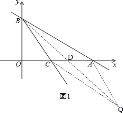
设点![]() 的坐标是
的坐标是![]() ,
,
∵ ![]() ,
,
∴ ![]() ①,
①,
∵ 四边形![]() 是平行四边形,
是平行四边形,
∴ 点![]() 是
是![]() 、
、![]() 的中点,
的中点,
∴ ![]() ②,
②,
由①②,可得
![]()
∴ 点![]() 的坐标是
的坐标是![]() .
.
如图![]() ,
,![]() 、
、![]() 交于点
交于点![]() ,
,
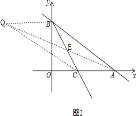
设点![]() 的坐标是
的坐标是![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∵ 四边形![]() 是平行四边形,
是平行四边形,
∴ 点![]() 是
是![]() 、
、![]() 的中点,
的中点,
∴ ![]() ,
,
解得![]() ,
,
∴ 点![]() 的坐标是
的坐标是![]() .
.
如图![]() ,
,![]() 、
、![]() 交于点
交于点![]() ,
,
设点![]() 的坐标是
的坐标是![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∵ 四边形![]() 是平行四边形,
是平行四边形,
∴ 点![]() 是
是![]() 、
、![]() 的中点,
的中点,
∴ ![]() ,
,
解得![]() ,
,
∴ 点![]() 的坐标是
的坐标是![]() .
.
综上,可得点![]() 的坐标是
的坐标是![]() 、
、![]() 或
或![]() .
.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目