题目内容
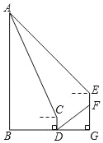
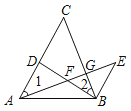
【题目】如图,D是AC上一点,BE∥AC,BE=AD,AE分别交BD、BC于点F、G,∠1=∠2.若DF=8,FG=4,则GE=_____.
【答案】12
【解析】
利用AAS判定△FEB≌△FAD,得BF=DF,根据有两组角对应相等的两个三角形相似,可得到△BFG∽△EFB,根据相似三角形的对应边成比例即可得到BF2=FGEF,由条件可求出EF长,则GE长可求出.
解:∵AD∥BE,
∴∠1=∠E.
又∠EFB=∠AFD,BE=AD,
∴△FEB≌△FAD;
∴BF=DF,
∵∠1=∠E,∠1=∠2,
∴∠2=∠E.
又∵∠GFB=∠BFE,
∴△BFG∽△EFB,
∴![]() ,
,
∴BF2=FGEF,
∴DF2=FGEF,
∵DF=8,FG=4,
∴EF=16,
∴GE=EF﹣FG=16﹣4=12.
故答案为:12.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目