[题目]按要求完成下列证明:已知:如图.AB∥CD.直线AE交CD于点C.∠BAC+∠CDF=180°. 求证:AE∥DF.证明: ∵AB∥CD( ) .∴∠BAC=∠DCE( ).∵∠BAC+∠CDF=180°(已知). ∴ +∠CDF=180°( ).∴AE∥DF( ). 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】按要求完成下列证明：

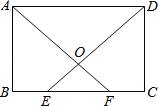
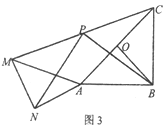
已知：如图，AB∥CD，直线AE交CD于点C，∠BAC+∠CDF=180°.

求证：AE∥DF.

证明： ∵AB∥CD（____________________________），

∴∠BAC=∠DCE（__________________________________________________________________________）.

∵∠BAC+∠CDF=180°(已知)，

∴____________ +∠CDF=180°（____________________________________）.

∴AE∥DF（______________________________________________________________________）.

【答案】已知两直线平行，同位角相等 ∠DCE 等量代换同旁内角互补，两直线平行

【解析】由AB∥CD得，∠BAC=∠DCE，又∠BAC+∠CDF=180°，则∠DCE+∠CDF=180°，根据平行线的判定定理，即可证得．

证明：∵AB∥CD（已知），

∴∠BAC=∠DCE（两直线平行，同位角相等）.

∵∠BAC+∠CDF=180°(已知)，

∴∠DCE+∠CDF=180°（等量代换）.

∴AE∥DF（同旁内角互补，两直线平行）.

练习册系列答案

相关题目

【题目】如图，在 △ABC 中，∠C=90°，DB⊥BC 于点，分别以点 D 和点为圆心，以大于的长为半径作弧，两弧相交于点 E 和点，作直线 EF，延长 AB 于点，连接 DG，下面是说明 ∠A=∠D 的说理过程，请把下面的说理过程补充完整：

因为 DB⊥BC（已知），

所以 ∠DBC=90°( ) ．

因为 ∠C=90°（已知），

所以 ∠DBC=∠C（等量代换），

所以 DB∥AC ( ) ，

所以（两直线平行，同位角相等）；

由作图法可知：直线 EF 是线段 DB 的 ( ) ，

所以 GD=GB，线段（上的点到线段两端点的距离相等），

所以 ( ) ，因为 ∠A=∠1（已知），

所以 ∠A=∠D（等量代换）．

【题目】（10分）如图，在矩形ABCD中，E，F为BC上两点，且BE=CF，连接AF，DE交于点O．

求证：（1）△ABF≌△DCE；

（2）△AOD是等腰三角形．

【题目】某班数学课外活动小组的同学欲测量公园内一棵树DE的高度，他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°，已知A点的高度AB为2米，台阶AC的坡度i=1：2，且B，C，E三点在同一条直线上，请根据以上条件求出树DE的高度．（测倾器的高度忽略不计，结果保留根号）

【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根，下列结论： ①b2﹣4ac＜0；②abc＞0；③a﹣b+c＜0；④m＞﹣2，
其中，正确的个数有（）

A.1
B.2
C.3
D.4

【题目】计算：（）﹣1﹣ +tan60°+|3﹣2 |．

【题目】对于平面直角坐标系xOy中的点A，给出如下定义：若存在点B（不与点A重合，且直线AB不与坐标轴平行或重合），过点A作直线m∥x轴，过点B作直线n∥y轴，直线m，n相交于点C.当线段AC，BC的长度相等时，称点B为点A 的等距点，称三角形ABC的面积为点A的等距面积. 例如：如图，点A（2，1），点B（5，4），因为AC= BC=3，所以B为点A 的等距点，此时点A的等距面积为.