��Ŀ����
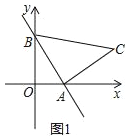
����Ŀ����֪����AOB�У�AB=BC=2,��ABC=90�㣬��O���߶�AC���е㣬����OB������AOB�Ƶ�A��ʱ����ת���ȵõ���ANM������CM����P���߶�CM���е㣬����PN��PB.
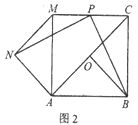
��1����ͼ1������=180��ʱ��ֱ��д���߶�PN��PB֮���λ�ù�ϵ��������ϵ��
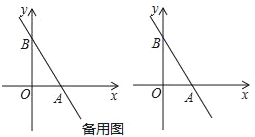
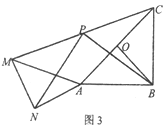
��2����ͼ2������=90��ʱ��̽���߶�PN��PB֮���λ�ù�ϵ��������ϵ��������������֤�����̣�
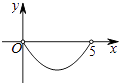
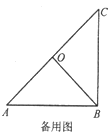
��3����ͼ3��ֱ��д������AOB���Ƶ�A��ʱ����ת�Ĺ����У��߶�PN�����ֵ����Сֵ��
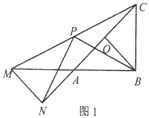
���𰸡�(1)PN=PB��PN��PB��(2)�ԣ�(3) ![]()
����������1������ת�����ʿɵ���ABC�ա�ANM,����ֱ��������б�ߵ����ߵ���б�ߵ�һ�룬�õ�PN��![]() ֮���λ�ù�ϵ��������ϵ����2������һ����֤���ķ����루1��һ������3������OP�����ù��ɶ����ɵó��߶�PN�����ֵ����Сֵ.
֮���λ�ù�ϵ��������ϵ����2������һ����֤���ķ����루1��һ������3������OP�����ù��ɶ����ɵó��߶�PN�����ֵ����Сֵ.
�⣺��![]() ��
��![]() ��
�� ![]() ��
��
��![]() ������
������![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
�� ![]() ��
��
��![]() ��
�� ![]() ,
,
�֡�![]() ,
,
���ı���![]() Ϊ�����Σ�
������
��![]() Ϊ
Ϊ![]() �е㣬
�е㣬 ![]() Ϊ
Ϊ![]() �е㣬
�е㣬
��![]() ��
��
��![]() ��
�� ![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
![]() ��
��![]() ��
��
��![]() ��
�� ![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ������
������![]() ��
��
��![]() ��
�� ![]() Ϊ
Ϊ![]() ��
�� ![]() �е㣬
�е㣬
��![]() ��
��
��![]() ����
����
��![]() ��
�� ![]() ��
��
��![]() ��
��
![]() ��
��
��![]() ��
��
��![]() ��
��
![]() ���ֵΪ
���ֵΪ![]() ����СֵΪ
����СֵΪ![]() ��
��

����Ŀ��ijˮ�����ؼƻ�װ�˼ס��ҡ�������ˮ����������ۣ�ÿ�������涨���أ�����ֻװһ��ˮ���������Ϊװ�˼ס��ҡ�������ˮ��������������
�� | �� | �� | |
ÿ��������װ���������֣� | 4 | 2 | 3 |
ÿ��ˮ���ɻ�����ǧԪ�� | 5 | 7 | 4 |
��1����8������װ���ҡ�������ˮ����22�ֵ�A�����ۣ���װ���ҡ�������ˮ������������������
��2��ˮ�����ؼƻ���20������װ�˼ס��ҡ�������ˮ����72�ֵ�B�����ۣ�ÿ��ˮ��������һ����������װ�˼�ˮ��������Ϊm������װ���ҡ�������ˮ�������������������������m��ʾ��
��3���ڣ�2���ʵĻ����ϣ���ΰ���װ�˿�ʹˮ�����ػ�����������������Ƕ��٣�