题目内容
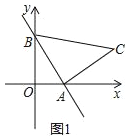
【题目】对于平面直角坐标系xOy中的点A,给出如下定义:若存在点B(不与点A重合,且直线AB不与坐标轴平行或重合),过点A作直线m∥x轴,过点B作直线n∥y轴,直线m,n相交于点C.当线段AC,BC的长度相等时,称点B为点A 的等距点,称三角形ABC的面积为点A的等距面积. 例如:如图,点A(2,1),点B(5,4),因为AC= BC=3,所以B为点A 的等距点,此时点A的等距面积为![]() .
.
(1)点A的坐标是(0,1),在点B1(-1,0),B2(2,3),B3(-1,-1)中,点A 的等距点为________________.
(2)点A的坐标是(-3,1),点A的等距点B在第三象限,
①若点B的坐标是![]() ,求此时点A的等距面积;
,求此时点A的等距面积;
②若点A的等距面积不小于![]() ,求此时点B的横坐标t的取值范围.
,求此时点B的横坐标t的取值范围.

【答案】B1, B2
【解析】(1)根据题目示例即可判断出点A的等距点为B1, B2 ;
(2)①分别求出AC,BC的长,利用三角形的面积计算公式即可求出点A的等距面积;
②分点B在点A左右两侧时进行计算求解即可.
(1)B1, B2 .
(2)①如图,根据题意,可知AC⊥BC.
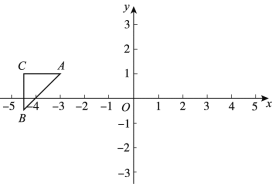
∵A(-3,1),B(![]() ,
,![]() ),
),
∴AC=BC=![]() .
.
∴三角形ABC的面积为![]() .
.
∴点A的等距面积为![]() .
.
②当点B左侧时,如图,
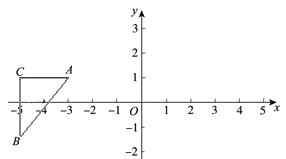
则有AC=BC=-3-t,
∵点A的等距面积不小于![]() ,
,
∴![]() ≥
≥![]() ,即
,即![]() ≥
≥![]() ,
,
∴![]() ;
;
当点B在点A的右侧时,如图,
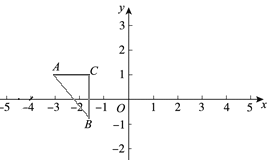
∵点B在第三象限,
同理可得,![]() .
.
故点B的横坐标t的取值范围是![]() 或
或![]() .
.

 计算高手系列答案
计算高手系列答案【题目】某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.
甲 | 乙 | 丙 | |
每辆汽车能装的数量(吨) | 4 | 2 | 3 |
每吨水果可获利润(千元) | 5 | 7 | 4 |
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?