题目内容
【题目】钝角三角形ABC中,∠BAC>90°,AB=AC,∠ACB=α,过点A的直线l交BC边于点D.点E在直线l上,且BC=BE.,点E在AD延长线上.
①当α=30°,点D恰好为BC中点时,补全图1直接写出∠BAE= °,
∠BEA= °;
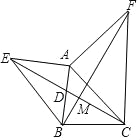
②如图2,若∠BAE=2α,求∠BEA的度数(用含α的代数式表示);
【答案】①60,30;②∠BEA=α
【解析】
①只要证明AE⊥BC,△BCE是等边三角形即可解决问题.②如图2中,延长CA到F,使得BF=BC,则BF=BE=BC,连接BF,作BM⊥AF于M,BN⊥AE于N.
只要证明Rt△BMF≌Rt△BNE,推出∠BEA=∠F,由BF=BC,推出∠F=∠C=α,推出∠BEA=α即可.
解:(1)①补全图1,如图所示.
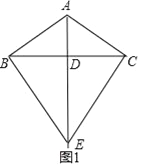
∵AB=AC,BD=DC,
∴AE⊥BC,
∴EB=EC,∠ADB=90°,
∵∠ABC=30°,
∴∠BAE=60°
∵BC=BE,
∴△BCE是等边三角形,∠DEB=∠DEC,
∴∠BEC=60°,∠BEA=30°
故答案为60,30.
②如图2中,延长CA到F,使得BF=BC,则BF=BE=BC,连接BF,作BM⊥AF于M,BN⊥AE于N.
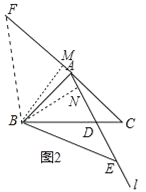
∵AB=AC,
∴∠ABC=∠C=α,
∴∠MAB=2α,∵∠BAN=2α,
∴∠BAM=∠BAN,
∴BM=BN,
在Rt△BMF和Rt△BNE中,
![]() ,
,
∴Rt△BMF≌Rt△BNE.
∴∠BEA=∠F,
∵BF=BC,
∴∠F=∠C=α,
∴∠BEA=α.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目