题目内容
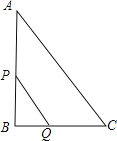
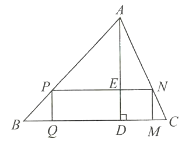
【题目】如图所示,![]() 是一块锐角三角形余料,边
是一块锐角三角形余料,边![]() 毫米,高
毫米,高![]() 毫米,要把它加工成一个矩形零件,使矩形的一边在
毫米,要把它加工成一个矩形零件,使矩形的一边在![]() 上,其余两个顶点分别在
上,其余两个顶点分别在![]() ,
,![]() 上,设该矩形的长
上,设该矩形的长![]() 毫米,宽
毫米,宽![]() 毫米.
毫米.
(1)求证:![]() ;
;
(2)当![]() 与
与![]() 分别取什么值时,矩形
分别取什么值时,矩形![]() 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
(3)当矩形![]() 的面积最大时,它的长和宽是关于
的面积最大时,它的长和宽是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,而
的两个根,而![]() ,
,![]() 的值又恰好分别是
的值又恰好分别是![]() ,10,12,13,
,10,12,13,![]() 这5个数据的众数与平均数,试求
这5个数据的众数与平均数,试求![]() 与
与![]() 的值.
的值.
【答案】(1)详见解析;(2)当![]() 毫米,
毫米,![]() 毫米时,矩形
毫米时,矩形![]() 面积最大,最大面积为2400平方毫米;(3)a=10,b=15或a=15,b=10.
面积最大,最大面积为2400平方毫米;(3)a=10,b=15或a=15,b=10.
【解析】
(1)易证△APN∽△ABC,根据相似三角形对应边的比等于对应高的比,即可求解;
(2)矩形PQMN的面积S=xy,根据(1)中y与x的函数关系式,即可得到S与x之间的函数关系,根据函数的性质即可求解;
(3)根据(2)中求得的长与宽的数值,利用根与系数的关系即可求得p,q的数值,根据众数与中位数的定义即可求得a与b的值.
(1)证明:根据已知条件易知:PN∥BC,AE⊥PN,PN=QM=y,DE=MN=x,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ;
;
(2)解:设矩形PQMN的面积为S,则
![]() ,
,![]() ,
,
∴当![]() 时,
时,![]() 有最大值2400,
有最大值2400,
此时![]() ,故当
,故当![]() 毫米,
毫米,![]() 毫米时,矩形
毫米时,矩形![]() 面积最大,最大面积为2400平方毫米;
面积最大,最大面积为2400平方毫米;
(3)解:由根与系数的关系,得![]() ,解得
,解得![]() ,
,
∵![]() ,10,12,13,
,10,12,13,![]() 众数为10,
众数为10,
∴![]() 或
或![]() ,
,
当![]() 时,有
时,有![]() ,解得
,解得 ![]() ,
,
当![]() 时,同理可得
时,同理可得![]() .
.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目