题目内容
【题目】抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式.
(2)一动点P在(1)中抛物线上滑动且满足S△ABP=10,求此时P点的坐标.
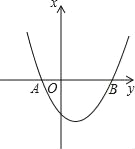
【答案】(1) y=x2﹣2x﹣3(2) m=5或﹣5.P的坐标是(-2,5)或(4,5);
【解析】
(1)把A、B的坐标代入函数解析式,即可得到关于b,c的方程组,从而求得b,c的值,求得函数的解析式;
(2)根据三角形的面积公式求得三角形的高,即P的纵坐标,代入解析式求得横坐标即可.
(1)根据题意得:![]()
解得:![]() ,
,
则方程的解析式是:y=x2﹣2x﹣3;
(2)AB=3+1=4,
设P的纵坐标是m,
则![]() ×4|m|=10,
×4|m|=10,
解得:|m|=5,
则m=5或﹣5.
当m=5时,x2-2x-3=5,x=-2或4,则P的坐标是(-2,5)或(4,5);
当m=-5时,x2-2x-3=-5,方程无解.
故P的坐标是(-2,5)或(4,5).

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
【题目】名闻遐迩的采花毛尖明前茶,成本每厅400元,某茶场今年春天试营销,每周的销售量y(斤)是销售单价x(元/斤)的一次函数,且满足如下关系:
x(元/斤) | 450 | 500 | 600 |
y(斤) | 350 | 300 | 200 |
(1)请根据表中的数据求出y与x之间的函数关系式;
(2)若销售每斤茶叶获利不能超过40%,该茶场每周获利不少于30000元,试确定销售单价x的取值范围.