题目内容
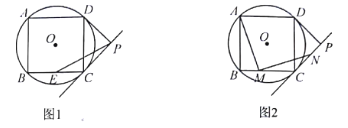
【题目】如图,四边形![]() 是
是![]() 的内接正方形,
的内接正方形,![]() ,
,![]() 、
、![]() 是
是![]() 的两 条切线,
的两 条切线,![]() 、
、![]() 为切点.
为切点.
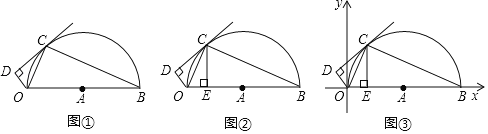
(1)如图1,求![]() 的半径;
的半径;
(2)如图1,若点![]() 是
是![]() 的中点,连结
的中点,连结![]() ,求
,求![]() 的长度;
的长度;
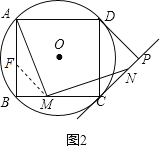
(3)如图2,若点![]() 是
是![]() 边上任意一点(不含
边上任意一点(不含![]() 、
、![]() ),以点
),以点![]() 为直角顶点,在
为直角顶点,在![]() 的上方作
的上方作![]() ,交直线
,交直线![]() 于点
于点![]() ,求证:
,求证:![]() .
.
【答案】(1)2![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)利用切线的性质以及正方形的判定与性质得出⊙O的半径即可;
(2)利用垂径定理得出OE⊥BC,∠OCE=45°,进而利用勾股定理得出即可;
(3)在AB上截取BF=BM,利用(1)中所求,得出∠ECP=135°,再利用全等三角形的判定与性质得出即可.
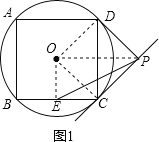
解:(1)如图1,连接OD,OC,
∵PC、PD是⊙O的两条切线,C、D为切点,
∴∠ODP=∠OCP=90°,
∵四边形ABCD是⊙O的内接正方形,
∴∠DOC=90°,OD=OC,
∴四边形DOCP是正方形,
∵AB=4,∠ODC=∠OCD=45°,
∴DO=CO=DCsin45°= ![]() ×4=2
×4=2 ![]() ;
;
(2)如图1,连接EO,OP,
∵点E是BC的中点,
∴OE⊥BC,∠OCE=45°,
则∠E0P=90°,
∴EO=EC=2,OP=![]() CO=4,
CO=4,
∴PE=![]() ;
;
(3)证明:如图2,在AB上截取BF=BM,
∵AB=BC,BF=BM,
∴AF=MC,∠BFM=∠BMF=45°,
∵∠AMN=90°,
∴∠AMF+∠NMC=45°,∠FAM+∠AMF=45°,
∴∠FAM=∠NMC,
∵由(1)得:PD=PC,∠DPC=90°,
∴∠DCP=45°,
∴∠MCN=135°,
∵∠AFM=180°-∠BFM=135°,
在△AFM和△CMN中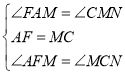
∴△AFM≌△CMN(ASA),
∴AM=MN.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目