ΧβΡΩΡΎ»ί
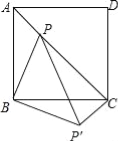
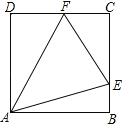
ΓΨΧβΡΩΓΩ»γΆΦΘ§RtΓςABC÷–Θ§ΓœBΘΫ90ΓψΘ§ACΘΫ10cmΘ§BCΘΫ6cmΘ§œ÷”–ΝΫΗωΕ·ΒψPΓΔQΖ÷±π¥”ΒψAΚΆΒψBΆ§ ±≥ωΖΔΘ§Τδ÷–ΒψP“‘2cm/sΒΡΥΌΕ»Θ§―ΊABœρ÷’ΒψB“ΤΕ·ΘΜΒψQ“‘1cm/sΒΡΥΌΕ»―ΊBCœρ÷’ΒψC“ΤΕ·Θ§Τδ÷–“ΜΒψΒΫ÷’ΒψΘ§Νμ“ΜΒψ“≤Υφ÷°ΆΘ÷ΙΘ°Ν§Ϋ”PQΘ°…ηΕ·Βψ‘ΥΕ· ±ΦδΈΣxΟκΘ°
Θ®1Θ©”ΟΚ§xΒΡ¥ζ ΐ Ϋ±μ ΨBQΓΔPBΒΡ≥ΛΕ»ΘΜ
Θ®2Θ©Β±xΈΣΚΈ÷Β ±Θ§ΓςPBQΈΣΒ»―ϋ»ΐΫ«–ΈΘΜ
Θ®3Θ© «Ζώ¥φ‘ΎxΒΡ÷ΒΘ§ ΙΒΟΥΡ±Ώ–ΈAPQCΒΡΟφΜΐΒ»”Ύ20cm2ΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ω¥Υ ±xΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
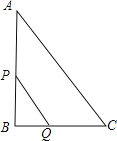
ΓΨ¥πΑΗΓΩΘ®1Θ©BQΘΫxΘ§PBΘΫ8©¹2xΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©¥φ‘ΎΘ§xΘΫ2.
ΘΜΘ®3Θ©¥φ‘ΎΘ§xΘΫ2.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί¬Ζ≥Χ=ΥΌΕ»ΓΝ ±Φδ«σ≥ωBQΘ§APΘ§‘ΌΗυΨίPB=AB-APΦ¥Ω….
Θ®2Θ©ΗυΨίΧβ“βΘ§Β±ΓςPBQΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§BQ=PBΘ§Ϋ®ΝΔ“ΜΗωΙΊ”ΎxΒΡΖΫ≥ΧΘ§ΫβΖΫ≥ΧΦ¥Ω….
Θ®3Θ©”ΟΚ§xΒΡ¥ζ ΐ Ϋ±μ Ψ≥ωΥΡ±Ώ–ΈAPQCΒΡΟφΜΐΘ§άϊ”ΟΥΡ±Ώ–ΈAPQCΒΡΟφΜΐΈΣ20Ϋ®ΝΔ“ΜΗωΙΊ”ΎxΖΫ≥ΧΘ§ΫβΖΫ≥ΧΦ¥Ω….»τ”–ΫβΘ§‘ρ¥φ‘ΎΘ§»τΈόΫβ‘ρ≤Μ¥φ‘Ύ.
ΫβΘΚΘ®1Θ©ΓΏΓœBΘΫ90ΓψΘ§ACΘΫ10Θ§BCΘΫ6Θ§
ΓύABΘΫ8Θ°
ΓύBQΘΫxΘ§PB=AB-APΘΫ8©¹2xΘΜ
Θ®2Θ©”…Χβ“βΘ§ΒΟ
8©¹2xΘΫxΘ§
ΓύxΘΫ![]() Θ°
Θ°
ΓύΒ±xΘΫ![]() ±Θ§ΓςPBQΈΣΒ»―ϋ»ΐΫ«–ΈΘΜ
±Θ§ΓςPBQΈΣΒ»―ϋ»ΐΫ«–ΈΘΜ
Θ®3Θ©ΦΌ…η¥φ‘ΎxΒΡ÷ΒΘ§ ΙΒΟΥΡ±Ώ–ΈAPQCΒΡΟφΜΐΒ»”Ύ20cm2Θ§
‘ρ![]()
ΫβΒΟx1ΘΫx2ΘΫ2Θ°
ΦΌ…η≥…ΝΔΘ§Υυ“‘Β±xΘΫ2 ±Θ§ΥΡ±Ώ–ΈAPQCΟφΜΐΒΡΟφΜΐΒ»”Ύ20cm2Θ°