题目内容
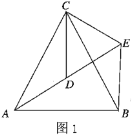
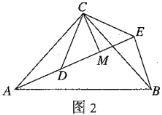
【题目】如图,在△ABC中,AG⊥BC,垂足为点G,点E为边AC上一点,BE=CE,点D为边BC上一点,GD=GB,连接AD交BE于点F.
(1)求证:∠ABE=∠EAF;
(2)求证:AE2=EFEC;
(3)若CG=2AG,AD=2AF,BC=5,求AE的长.
【答案】(1)见解析;(2)见解析;(3)AE=![]() .
.
【解析】
(1)首先证明∠EBC=∠C,∠ABD=∠ADB,再根据∠ABD=∠ABE+∠EBC,∠ADB=∠DAC+∠C,可得结论.
(2)证明△AEF∽△BEA可得结论.
(3)设BE交AG于J,连接DJ,DE.证明四边形AJDE是平行四边形,推出DE⊥BC,AE=DJ,想办法求出DJ即可解决问题.
(1)证明:∵EB=EC,
∴∠EBC=∠C,
∵AG⊥BD,BG=GD,
∴AB=AD,
∴∠ABD=∠ADB,
∵∠ABD=∠ABE+∠EBC,∠ADB=∠DAC+∠C,
∴∠ABE=∠DAC,
即∠ABE=∠EAF;
(2)证明:∵∠AEF=∠BEA,∠EAF=∠ABE,
∴△AEF∽△BEA,
∴![]() ,
,
∴AE2=EFEB,
∵EB=EC,
∴AE2=EFEC;
(3)解:设BE交AG于J,连接DJ,DE.
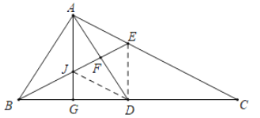
∵AG垂直平分线段BD,
∴JB=JD,
∴∠JBD=∠JDG,
∵∠JBD=∠C,
∴∠JDB=∠C,
∴DJ∥AC,
∴∠AEF=∠DJF,
∵AD=2AF,
∴AF=DF,
在△AFE和△DFJ中,
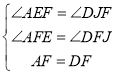 ,
,
∴△AFE≌△DFJ(AAS),
∴EF=FJ,AE=DJ,
∵AF=DF,
∴四边形AJDE是平行四边形,
∴DE∥AG,
∵AG⊥BC,
∴ED⊥BC,
∵EB=EC,
∴BD=DC=![]() ,
,
∴BG=DG=![]() ,
,
∵tan∠JDG=tan∠C=![]() ,
,
∴JG=![]() ,
,
∵∠JGD=90°,
∴DJ= ,
,
∴AE=DJ=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目