ЬтФПФкШн
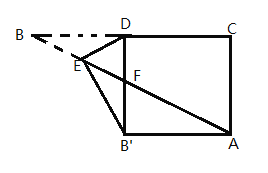
ЁОЬтФПЁПШчЭМ1ЃЌЁїABCЃЈ![]() ACЃМBCЃМACЃЉШЦЕуCЫГЪБеыа§зЊЕУЁїDECЃЌЩфЯпABНЛЩфЯпDEгкЕуFЃЎ
ACЃМBCЃМACЃЉШЦЕуCЫГЪБеыа§зЊЕУЁїDECЃЌЩфЯпABНЛЩфЯпDEгкЕуFЃЎ
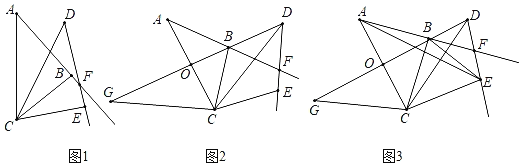
ЃЈ1ЃЉЁЯAFDгыЁЯBCEЕФЙиЯЕЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБа§зЊНЧЮЊ60ЁуЪБЃЌЕуDЃЌЕуBгыЯпЖЮACЕФжаЕуOЧЁКУдкЭЌвЛжБЯпЩЯЃЌбгГЄDOжСЕуGЃЌЪЙOGЃНODЃЌСЌНгGCЃЎ
ЂйЁЯAFDгыЁЯGCDЕФЙиЯЕЪЧЁЁ ЁЁЃЌЧыЫЕУїРэгЩЃЛ
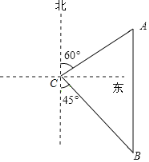
ЂкШчЭМ3ЃЌСЌНгAEЃЌBEЃЌШєЁЯACBЃН45ЁуЃЌCEЃН4ЃЌЧѓЯпЖЮAEЕФГЄЖШЃЎ
ЁОД№АИЁПЃЈ1ЃЉЁЯAFDЃНЁЯBCEЃЛЃЈ2ЃЉЂйЁЯAFDЃН![]() ЁЯGCDЛђЁЯAFD+ЁЯGCDЃН180ЁуЃЛЂк2
ЁЯGCDЛђЁЯAFD+ЁЯGCDЃН180ЁуЃЛЂк2![]() +2
+2![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШХаЖЯГіЁЯBCEЃНЁЯACDЃЌдйРћгУШ§НЧаЮЕФФкНЧКЭЖЈРэЃЌХаЖЯГіЁЯACDЃНЁЯAFDЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЂйЯШХаЖЯГіЁЯACDЪЧЕШБпШ§НЧаЮЃЌЕУГіADЃНCDЃЌдйХаЖЯГіЁЯACDЃНЁЯAFDЃЌНјЖјХаЖЯГіЁїAODЁеЁїCOGЃЈSASЃЉЃЌЕУГіADЃНCGЃЌМДПЩЕУГіНсТлЃЛ
ЂкЯШХаЖЯГіЁЯGCBЃНЁЯBCEЃЌНјЖјХаЖЯГіЁЯGCBЃНЁЯACEЃЌНјЖјХаЖЯГіЁїGCBЁеЁїACEЃЌЕУГіBCЃНCEЃН4ЃЌзюКѓгУШёНЧШ§НЧКЏЪ§МДПЩЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌ

AFгыCDЕФНЛЕуМЧзїЕуNЃЌгЩа§зЊжЊЃЌЁЯACBЃНЁЯDCEЃЌЁЯAЃНЁЯDЃЌ
ЁрЁЯBCEЃНЁЯACDЃЌ
ЁпЁЯACDЃН180ЁуЉЁЯAЉЁЯANCЃЌЁЯAFDЃН180ЁуЉЁЯDЉЁЯDNFЃЌЁЯANCЃНЁЯDNFЃЌ
ЁрЁЯACDЃНЁЯAFDЃЌ
ЁрЁЯAFDЃНЁЯBCEЃЌ
ЙЪД№АИЮЊЃКЁЯAFDЃНЁЯBCEЃЛ
ЃЈ2ЃЉЂйЁЯAFDЃН![]() ЁЯGCDЛђЁЯAFD+ЁЯGCDЃН180ЁуЃЌ
ЁЯGCDЛђЁЯAFD+ЁЯGCDЃН180ЁуЃЌ
РэгЩЃКШчЭМ2ЃЌСЌНгADЃЌгЩа§зЊжЊЃЌЁЯCABЃНЁЯCDEЃЌCAЃНCDЃЌЁЯACDЃН60ЁуЃЌ

ЁрЁїACDЪЧЕШБпШ§НЧаЮЃЌЁрADЃНCDЃЌ
ЁпЁЯAMCЃНЁЯDMFЃЌ
ЁрЁїACMЁзЁїDFMЃЌ
ЁрЁЯACDЃНЁЯAFDЃЌ
ЁпOЪЧACЕФжаЕуЃЌ
ЁрAOЃНCOЃЌ
ЁпODЃНOGЃЌЁЯAODЃНЁЯCOGЃЌ
ЁрЁїAODЁеЁїCOGЃЈSASЃЉЃЌ
ЁрADЃНCGЃЌ
ЁрCGЃНCDЃЌ
ЁрЁЯGCDЃН2ЁЯACDЃН120ЁуЃЌ
ЁрЁЯAFDЃН![]() ЁЯGCDЛђЁЯAFD+ЁЯGCDЃН180ЁуЃЌ
ЁЯGCDЛђЁЯAFD+ЁЯGCDЃН180ЁуЃЌ
ЙЪД№АИЮЊЃКЁЯAFDЃН![]() ЁЯGCDЛђЁЯAFD+ЁЯGCDЃН180ЁуЃЛ
ЁЯGCDЛђЁЯAFD+ЁЯGCDЃН180ЁуЃЛ
ЂкгЩЂйжЊЃЌЁЯGCDЃН120ЁуЃЌЁЯACDЃНЁЯBCEЃН60ЁуЃЌ
ЁрЁЯGCAЃНЁЯGCDЉЁЯACDЃН60ЁуЃЌ
ЁрЁЯGCAЃНЁЯBCEЃЌ
ЁпЁЯGCBЃНЁЯGCA+ЁЯACBЃЌЁЯACEЃНЁЯBCE+ЁЯACBЃЌ
ЁрЁЯGCBЃНЁЯACEЃЌ
гЩЂйжЊЃЌCGЃНCDЃЌCDЃНCAЃЌ
ЁрCGЃНCAЃЌ
ЁпBCЃНECЃН4ЃЌ
ЁрЁїGCBЁеЁїACEЃЈSASЃЉЃЌ
ЁрGBЃНAEЃЌ
ЁпCGЃНCDЃЌOGЃНODЃЌ
ЁрCOЁЭGDЃЌ
ЁрЁЯCOGЃНЁЯCOBЃН90Ёу
дкRtЁїBOCжаЃЌBOЃНBCsinЁЯACBЃН2![]() ЃЌCOЃНBCcosЁЯACBЃН2
ЃЌCOЃНBCcosЁЯACBЃН2![]() ЃЌ
ЃЌ
дкRtЁїGOCжаЃЌGOЃНCOtanЁЯGCAЃН2![]() ЃЌ
ЃЌ
ЁрGBЃНCO+BOЃН2![]() +2
+2![]() ЃЌ
ЃЌ
ЁрAEЃН2![]() +2
+2![]() ЃЎ
ЃЎ

ЁОЬтФПЁПЮЊСЫгНгЬхг§жаПМЃЌГѕШ§7АрЕФЬхг§РЯЪІЖдШЋАр48УћбЇЩњНјааСЫвЛДЮЬхФмФЃФтВтЪдЃЌЕУЗжОљЮЊећЪ§ЃЌТњЗж10ЗжЃЌГЩМЈДяЕН6ЗжвдЩЯЃЈАќРЈ6ЗжЃЉЮЊКЯИёЃЌГЩМЈДяЕН9ЗжвдЩЯЃЈАќРЈ9ЗжЃЉЮЊгХауЃЌетДЮФЃФтВтЪджаФаЁЂХЎЩњШЋВПГЩМЈЗжВМЕФЬѕаЮЭГМЦЭМШчЯТ
ЃЈ1ЃЉЧыВЙГфЭъГЩЯТУцЕФГЩМЈЭГМЦЗжЮіБэЃК
ЦНОљЗж | ЗНВю | жаЮЛЪ§ | КЯИёТЪ | гХауТЪ | |
ФаЩњ | 6.9 | 2.4 | ______ | 91.7% | 16.7% |
ХЎЩњ | ______ | 1.3 | ______ | 83.3% | 8.3% |
ЃЈ2ЃЉФаЩњЫЕЫћУЧЕФКЯИёТЪЁЂгХауТЪОљИпгкХЎЩњЃЌЫљвдЫћУЧЕФГЩМЈКУгкХЎЩњЃЌЕЋХЎЩњВЛЭЌвтФаЩњЕФЫЕЗЈЃЌШЯЮЊХЎЩњЕФГЩМЈвЊКУгкФаЩњЃЌЧыИјГіСНЬѕжЇГжХЎЩњЙлЕуЕФРэгЩЃЛ
ЃЈ3ЃЉЬхг§РЯЪІЫЕЃЌдлАрЕФКЯИёТЪЛљБОДяБъЃЌЕЋгХауТЪЬЋЕЭЃЌЮвУЧБиаыМгЧПЬхг§ЖЭСЖЃЌСНжмКѓЕФФПБъЪЧЃКШЋАргХауТЪДяЕН50%ЃЎШчЙћХЎЩњаТдігХауШЫЪ§ЧЁКУЪЧФаЩњаТдігХауШЫЪ§ЕФСНБЖЃЌФЧУДФаЁЂХЎЩњЗжБ№аТдіЖрЩйгХауШЫЪ§ВХФмДяЕНРЯЪІЕФФПБъЃП