题目内容
【题目】如图,在平行四边形ABCD中,AQ、BN、CN、DQ分別是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AQ与BN相交于点P,CN与DQ相交于点M,判断四边形MNPQ的形状,并证明你的结论.
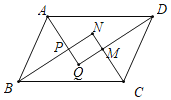
【答案】四边形MNPQ是矩形,理由见解析.
【解析】
可得出一个结论,即“四边形PQMN为矩形”.因为平行四边形中邻角互补,所以其每两个相邻内角的平分线都互相垂直,从而根据有三个角是直角的四边形是矩形来判定.
四边形MNPQ是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB+∠ABC=180°,
∵AP,BN分别平分∠DAB,∠ABC,
∴∠PAB+∠PBA=![]() (∠DAB+∠ABC)=×180°=90°,
(∠DAB+∠ABC)=×180°=90°,
∴∠NPQ=∠APB=90°,
同理:∠N=90°,∠AQD=90°,
∴四边形MNPQ是矩形.

练习册系列答案
相关题目