题目内容
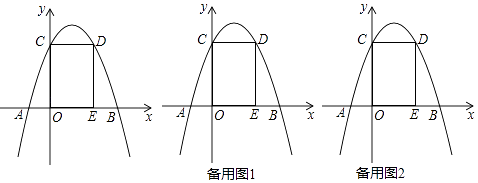
【题目】已知I是△ABC的内心,AI延长线交△ABC外接圆于D,连BD.
(1)在图1中,求证:DB=DI;
(2)如图2,若AB为直径,且OI⊥AD于I点,DE切圆于D点,求sin∠ADE的值.
【答案】
(1)解:连接BI,

∵I是△ABC的内心,
∴AD平分∠CAB,BI平分∠ABC,
∴∠CAD=∠BAD,∠ABI=∠CBI,
∵∠CAD=∠DBC,
∴∠DAB=∠CBD,
∵∠DBI=∠DBC+∠CBI,
∠DIB=∠DAB+∠IBA,
∴∠DIB=∠DBI,
∴BD=DI;
(2)解:连接BD,

∵AB为直径,
∴∠ADB=90°,
∵OI⊥AD,
∴AD=2DI,
∵BD=DI,
∴AD=2BD,
∴AB= ![]() =
= ![]() BD,
BD,
∵DE切圆于D点,
∴∠ABD=∠ADE,
∴sin∠ADE=sin∠ABD= ![]() =
= ![]() .
.
【解析】(1)连接BI,依据三角形的内心的定义可得到AD平分∠CAB,BI平分∠ABC,根据角平分线的定义得到∠CAD=∠BAD,∠ABI=∠CBI,得到结合圆周角定理可得到∠DAB=∠CBD,然后再依据三角形的外角的性质得到∠DIB=∠DBI,最后,依据等角对等边的性质可得到BD=DI;
(2)连接BD,根据圆周角定理的推理可得到∠ADB=90°,然后再依据垂径定理得到AD=2DI,接下来,利用勾股定理求得AB的长,,根据弦切角定理得到∠ABD=∠ADE,接下来,依据锐角三角函数的定义求解即可.
【考点精析】利用圆周角定理对题目进行判断即可得到答案,需要熟知顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
相关题目