题目内容
【题目】已知直线AB∥CD.
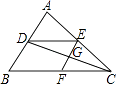
(1)如图1,请直接写出∠BME、∠E、∠END的数量关系为 ;
(2)如图2,∠BME与∠CNE的角平分线所在的直线相交于点P,试探究∠P与∠E之间的数量关系,并证明你的结论;
(3)如图3,∠ABM=![]() ∠MBE,∠CDN=
∠MBE,∠CDN=![]() ∠NDE,直线MB、ND交于点F,则
∠NDE,直线MB、ND交于点F,则![]() =___.
=___.

【答案】(1)∠E=∠END-∠BME;(2)∠E+2∠NPM=180°,证明见解析;(3)![]() .
.
【解析】
(1)由AB∥CD,即可得到∠END=∠EFB,再根据∠EFB是△MEF的外角,即可得出∠E=∠EFB-∠BME=∠END-∠BME;
(2)由平行线的性质以及三角形外角性质,即可得到∠NPM=∠NGB+∠PMA=∠CNP+∠PMA,再根据三角形内角和定理,即可得到∠E+2∠PMA+2∠CNP=180°,即∠E+2(∠PMA+∠CNP)=180°,即可得到∠E+2∠NPM=180°;
(3)延长AB交DE于G,延长CD交BF于H,由平行线的性质以及三角形外角性质,即可得到∠E=∠ABE-∠AGE=∠ABE-∠CDE;依据∠CHB是△DFH的外角,即可得到∠F=∠CHB-∠FDH=![]() ∠ABE-
∠ABE-![]() ∠CDE=
∠CDE=![]() (∠ABE-∠CDE),进而得出∠F=
(∠ABE-∠CDE),进而得出∠F=![]() ∠E.
∠E.
解:(1)如图1,∵AB∥CD,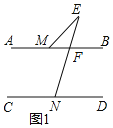
∴∠END=∠EFB,
∵∠EFB是△MEF的外角,
∴∠E=∠EFB-∠BME=∠END-∠BME,
故答案为:∠E=∠END-∠BME;
(2)如图2,∵AB∥CD,
∴∠CNP=∠NGB,
∵∠NPM是△GPM的外角,
∴∠NPM=∠NGB+∠PMA=∠CNP+∠PMA,
∵MQ平分∠BME,NP平分∠CNE,
∴∠CNE=2∠CNP,∠FME=2∠BMQ=2∠PMA,
∵AB∥CD,
∴∠MFE=∠CNE=2∠CNP,
∵△EFM中,∠E+∠FME+∠MFE=180°,
∴∠E+2∠PMA+2∠CNP=180°,
即∠E+2(∠PMA+∠CNP)=180°,
∴∠E+2∠NPM=180°;
(3)如图3,延长AB交DE于G,延长CD交BF于H,
∵AB∥CD,
∴∠CDG=∠AGE,
∵∠ABE是△BEG的外角,
∴∠E=∠ABE-∠AGE=∠ABE-∠CDE,①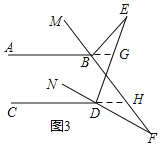
∵∠ABM=![]() ∠MBE,∠CDN=
∠MBE,∠CDN=![]() ∠NDE,
∠NDE,
∴∠ABM=![]() ∠ABE=∠CHB,∠CDN=
∠ABE=∠CHB,∠CDN=![]() ∠CDE=∠FDH,
∠CDE=∠FDH,
∵∠CHB是△DFH的外角,
∴∠F=∠CHB-∠FDH=![]() ∠ABE-
∠ABE-![]() ∠CDE=
∠CDE=![]() (∠ABE-∠CDE),②
(∠ABE-∠CDE),②
由①代入②,可得∠F=![]() ∠E,
∠E,
即![]() =
=![]() .
.
故答案为:![]() .
.

 名校课堂系列答案
名校课堂系列答案