题目内容
【题目】如图，已知抛物线y=﹣x2+bx+c与x轴交于A，B与y轴交于C，过C作x轴的平行线交抛物线于点D，过点D作x轴的垂线交x轴于E，点D的坐标为（2，3）
（1）求抛物线的解析式；
（2）点P为第一象限直线DE右侧抛物线上一点，连接AP交y轴于点F，连接PD、DF，设点P的横坐标为t，△PFD的面积为S，求S与t的函数关系式；
（3）在（2）的条件下，点P向下平移3个单位得到点Q，连接AQ、EQ，若∠AQE=45°，求点P的横坐标．
【答案】
（1）解：由题意D（2，3），C（0，3），
∵CD∥x轴，
∴C、D关于对称轴对称，
∴对称轴x=1，
∴﹣ 
=1，
∴b=2，c=3，
∴抛物线的解析式为y=﹣x2+2x+3．
（2）解：如图1中，连接PC，作PH⊥AB于H．设P（t，﹣t2+2t+3）．
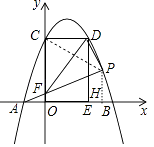
对于抛物线y=﹣x2+2x+3，令y=0，﹣x2+2x+3=0，解得x=﹣1或3，
∴A（﹣1，0），B（3，0）
∵OF∥PB，
∴ 
= 
，
∴FO=（﹣t2+2t+3） 
=3﹣t，
∴CF=3﹣（3﹣t）=t，
S=S△PCF+S△PCD﹣S△CDF= 
tt+ ×2×[3﹣（﹣t2+2t+3）]﹣ t2= 
t2﹣3t（2＜t＜3）．
（3）解：如图构造等腰直角三角形△AKE，使得AK=EK，∠AKE=90°，则易知K（ ，﹣ ），以K为圆心，AK为半径画⊙K．
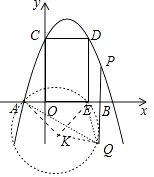
∵∠AQE=45°= ∠AKE，
∴点Q在⊙K上，设P（m，﹣m2+2m+3），则Q（m，﹣m2+2m），
∵AK=QK，
∴（1+ ）2+（ ）2=（m﹣ ）2+（﹣m2+2m+ ）2，
∴ 
+ =m2﹣m+ 
+（﹣m2+2m）2+3（﹣m2+2m）+ ，
∴m2﹣m﹣2+m2（m﹣2）2﹣3m（m﹣2）=0，
∴（m﹣2）（m+1）+m2（m﹣2）2﹣3m（m﹣2）=0，
∴（m﹣2）[（m+1）+m3﹣2m2﹣3m]=0，
∴（m﹣2）[（m+1）+m（m+1）（m﹣3）]=0，
∴（m﹣2）（m+1）（m2
∴m=2或﹣1或 
，
∵点P为第一象限直线DE右侧抛物线上一点，
∴m= 
，
∴满足条件的点P的横坐标为 ．
【解析】（1）根据题意易求得点C的坐标，再用待定系数法求出抛物线的解析式。或根据点C、D是两对称点，求出对称轴，即可求出抛物线的解析式。
（2）观察函数图像，可知S△PFD=S△PCF+S△PCD﹣S△CDF，因此连接PC，作PH⊥AB于H．设P（t，﹣t2+2t+3），再用含t的代数式分别求出△PCF、△PCD、△CDF的面积，就可以求出S与t的函数关系式。
（3）抓住已知∠AQE=45°，添加辅助线，构造圆周角为45°的圆心角，构造等腰直角三角形△AKE，使得AK=EK，∠AKE=90°，以K为圆心，AK为半径画⊙K，易得到K点坐标，得出点Q在圆上，设出点P、点Q的坐标，根据AK=QK。列出方程，求解即可求出点P的横坐标。
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对矩形的性质的理解，了解矩形的四个角都是直角，矩形的对角线相等．
