题目内容
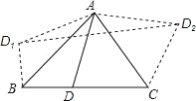
【题目】如图1,点![]() 为线段
为线段![]() 上一点,一副直角三角板的直角顶点与点
上一点,一副直角三角板的直角顶点与点![]() 重合,直角边
重合,直角边![]() 、
、![]() 在线段
在线段![]() 上,
上,![]() .
.
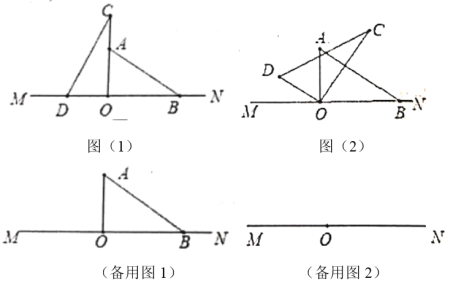
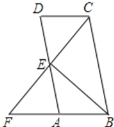
(1)将图1中的三角板![]() 绕着点
绕着点![]() 沿顺时针方向旋转到如图2所示的位置,若
沿顺时针方向旋转到如图2所示的位置,若![]() ,则
,则![]() ________;猜想
________;猜想![]() 与
与![]() 的数量关系为________;
的数量关系为________;
(2)将图1中的三角板![]() 绕着点
绕着点![]() 沿逆时针方向按每秒
沿逆时针方向按每秒![]() 的速度旋转一周,三角板
的速度旋转一周,三角板![]() 不动,请问几秒时
不动,请问几秒时![]() 所在的直线平分
所在的直线平分![]() ?
?
(3)将图1中的三角板![]() 绕着点
绕着点![]() 沿逆时针方向按每秒
沿逆时针方向按每秒![]() 的速度旋转一周,同时三角板
的速度旋转一周,同时三角板![]() 绕着点
绕着点![]() 沿顺时针方向按每秒
沿顺时针方向按每秒![]() 的速度旋转(随三角板
的速度旋转(随三角板![]() 停止而停止),请计算几秒时
停止而停止),请计算几秒时![]() 与
与![]() 的角分线共线.
的角分线共线.
【答案】(1)145°,180°;(2)3秒或15秒后OD所在的直线平分∠AOB;(3)![]() 秒或
秒或![]() 或
或![]() 秒后
秒后![]() 与
与![]() 的角分线共线.
的角分线共线.
【解析】
(1)根据互余关系先求出∠AOD,再由角的和差求出结果;
(2)当沿逆时针方向旋转45°或225°时,OD所在的直线平分∠AOB,由此便可求得结果;
(3)①当∠COD和∠AOB角平分线夹角为180时,②当∠COD和∠AOB角平分线重合时,即夹角为0°,③当∠COD和∠AOB角平分线重合后再次夹角为180°时,列出关于t的方程进行解答.
解:(1)∵∠COD=90°,∠AOC=35°,
∴∠AOD=∠COD-∠AOC=55°,
∵∠AOB=90°,
∴∠BOD=∠AOB+AOD=145°,
∵∠BOD=∠AOD+∠AOC+BOC,
∴∠AOC+∠BOD=∠AOC+∠AOD+∠AOC+∠BOC=∠COD+∠AOB=90°+90°=180°,
∴∠AOC+∠BOD=∠=180°,
故答案为:145°,180°;
(2)根据题意可得,
当旋转45°或225°时,OD所在的直线平分∠AOB,
所以,旋转时间为:45°÷15°=3(秒),225°÷15°=15(秒),
则3秒或15秒后OD所在的直线平分∠AOB;
(3)起始位置∠COD和∠AOB角平分线夹角为90°,
①当∠COD和∠AOB角平分线夹角为180时,
![]() ,
,
解得![]() (秒);
(秒);
②当∠COD和∠AOB角平分线重合时,即夹角为0°,
![]() ,
,
解得:![]() (秒);
(秒);
③当∠COD和∠AOB角平分线重合后再次夹角为180°时,
![]() ,
,
解得:![]() (秒);
(秒);
综上,![]() 秒或
秒或![]() 或
或![]() 秒后
秒后![]() 与
与![]() 的角分线共线.
的角分线共线.

【题目】白色污染( Whitepollution)是人们对难降解的塑料垃圾(多指塑料袋)污染环境现象的一种形象称谓.为了让全校同学感受丢弃塑料袋对环境的影响,小彬随机抽取某小区![]() 户居民,记录了这些家庭
户居民,记录了这些家庭![]() 年某个月丢弃塑料袋的数量(单位:个)
年某个月丢弃塑料袋的数量(单位:个)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请根据上述数据,解答以下问题:
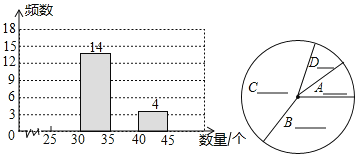
(1)小彬按“组距为![]() ”列出了如下的频数分布表(每组数据含最小值不含最大值),请将表中空缺的部分补充完整,并补全频数直方图;
”列出了如下的频数分布表(每组数据含最小值不含最大值),请将表中空缺的部分补充完整,并补全频数直方图;
分组 | 划记 | 频数 |
| _______ | ________ |
|
|
|
| _______ | ________ |
|
|
|
合计 | / |
|
(2)根据(1)中的直方图可以看出,这![]() 户居民家这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
户居民家这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
(3)根据频数分布表,小彬又画出了如图所示的扇形统计图.请将统计图中各组占总数的百分比填在图中,并求出![]() 组对应的扇形圆心角的度数;
组对应的扇形圆心角的度数;
(4)若该小区共有![]() 户居民家庭,请你估计每月丢弃的塑料袋数量不小于
户居民家庭,请你估计每月丢弃的塑料袋数量不小于![]() 个的家庭个数.
个的家庭个数.