题目内容
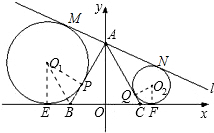
如图,等边△ABC的边长为6,BC在x轴上,BC边上的高线AO在y轴上,直线l绕点A转动(与线段BC没有 交点).设与AB、l、x轴相切的⊙O1的半径为r1,与AC、l、x轴相切的⊙O2半径为r2
交点).设与AB、l、x轴相切的⊙O1的半径为r1,与AC、l、x轴相切的⊙O2半径为r2
(1)求两圆的半径之和;
(2)探索直线l绕点A转动到什么位置时两圆的面积之和最小?最小值是多少?
(3)若r1-r2=
,求经过点O1、O2的一次函数解析式.
 交点).设与AB、l、x轴相切的⊙O1的半径为r1,与AC、l、x轴相切的⊙O2半径为r2
交点).设与AB、l、x轴相切的⊙O1的半径为r1,与AC、l、x轴相切的⊙O2半径为r2(1)求两圆的半径之和;
(2)探索直线l绕点A转动到什么位置时两圆的面积之和最小?最小值是多少?
(3)若r1-r2=
| 3 |
(1)解法1:设切点分别为M、N、E、F、P、Q,由切线定义,可得AM=AP,AN=AQ,EB=BP,FC=CQ,MN=EF,
∴MN+EF=18,MN=EF,
∴EF=9,
∴EB+FC=9-6=3,
∵∠EBP=120°,
∴∠EBO1=60°,
∴r1=
EB,
同理r2=
CF,
∴r1+r2=
(EB+FC)=3
,
解法2:∵∠EBP=120°,
∴∠EBO1=60°,
∴EB=PB=
r1,同理CF=CQ=
r2,
∴由EF=MN得:
r1+6+
r2=(6-
r1)+(6-
r2)
∴r1+r2=3
评分参考:①利用Rt△解得r与切线关系(2分);②得出结果r1+r2=3
,(2分)
(2)两圆面积之和S=π
+π(3
-r1)2=2π[(r1-
)2+
],(2分)
∴当r1=
时,面积之和最小,这时r1=r2,直线l∥x轴,(1分)
面积和的最小值为
π;(1分)
(3)由r1+r2=3
,r1-r2=
,解得O1(-5,2
),O2(4,
),(2分)
直线O1O2解析式为y=-
x+
.(2分)
∴MN+EF=18,MN=EF,
∴EF=9,
∴EB+FC=9-6=3,
∵∠EBP=120°,
∴∠EBO1=60°,
∴r1=
| 3 |
同理r2=
| 3 |
∴r1+r2=
| 3 |
| 3 |
解法2:∵∠EBP=120°,
∴∠EBO1=60°,
∴EB=PB=
| ||
| 3 |
| ||
| 3 |
∴由EF=MN得:
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
∴r1+r2=3
| 3 |
评分参考:①利用Rt△解得r与切线关系(2分);②得出结果r1+r2=3
| 3 |
(2)两圆面积之和S=π
| r | 21 |
| 3 |
3
| ||
| 2 |
| 27 |
| 4 |
∴当r1=
3
| ||
| 2 |
面积和的最小值为
| 27 |
| 2 |
(3)由r1+r2=3
| 3 |
| 3 |
| 3 |
| 3 |
直线O1O2解析式为y=-
| ||
| 9 |
13
| ||
| 9 |


练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目