Question

【题目】如图，为矩形对角线，的交点，，是直线上的动点，且，则的最小值是_________．

Answer 1

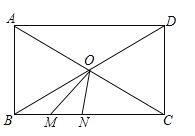
【答案】

【解析】

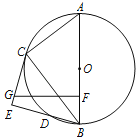
如图所示，作点O关于BC的对称点P，连接PM，将MP沿着MN的方向平移MN长的距离，得到NQ，连接PQ，则四边形MNQP是平行四边形;再利用平行四边形的性质以及轴对称的性质，可得当O，N，Q在同一直线上时，OM+ON的最小值等于OQ长，即可完成解答．

解：如图所示，作点O关于BC的对称点P，连接PM，将MP沿着MN的方向平移MN长的距离，得到NQ，连接PQ，则四边形MNQP是平行四边形，

∵MN=PQ=1，PM=NQ=MO，

∴OM+ON=QN+ON，

∴当O，N，Q在同一直线上时，OM+ON的最小值等于OQ长，

连接PO，交BC于E，

∴BC垂直平分OP，

又∵矩形ABCD中，OB=OC，

∴E是BC的中点，

∴OE是△ABC的中位线，

∴OE=AB=2，

∴OP=2×2=4，

又∵PQ//MN，

∴PQ⊥OP，

∴Rt△OPQ中，OQ=

∴OM+ON的最小值是；

故答案为：．