Question

【题目】如图，已知点、在双曲线上，轴于，轴于点，与交于点，是的中点．

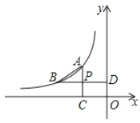
（1）试判断四边形的形状，并说明理由．

（2）若的面积为，求该双曲线的解析式．

Answer 1

【答案】（1）菱形，理由见解析；（2）．

【解析】

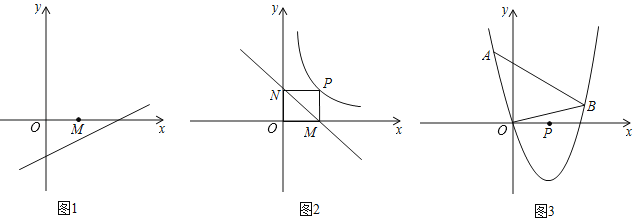
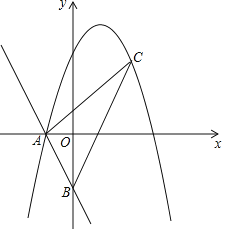
（1）连接AD、CD、BC；AC⊥x轴于C，BD⊥y轴于点D，则AC⊥BD；设A（m，n），则mn=k，P（m，n），再确定B点坐标，进而说明PD=PB，AP=PC， 即可判定四边形ABCD为菱形；

（2）由△ABP的面积为3，知BPAP=6.由反比例函数中k的几何意义，知本题k=OCAC，再由反比例函数的性质以及P是AC的中点的条件，得出OC=BP，AC=2AP，从而完成解答．

解:(1) 四边形ABCD为菱形,理由如下:

如图:连接AD、CD、BC；AC⊥x轴于C，BD⊥y轴于点D，

∴AC⊥BD；

设A（m，n），则mn=k，P（m，n），

B点纵坐标为n，横坐标为 ，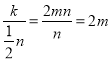

∴PD=PB，

又∵AP=PC，

∴四边形ABCD是菱形；

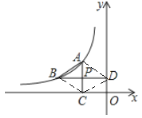
（2）∵△ABP的面积为·BP·AP=3，

∴BP·AP=6，

∵P是AC的中点，

∴A点的纵坐标是B点纵坐标的2倍，

又∵点A、B都在双曲线上，

∴B点的横坐标是A点横坐标的2倍，

∴OC=DP=BP，

∴|k| =OC·AC=BP·2AP=12.

又∵该函数图像在第二象限

∴k=-12

∴该双曲线的解析式是：.