题目内容
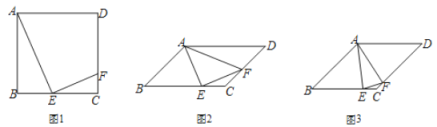
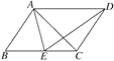
【题目】如图，在ABCD中，E为BC边上一点，且AB=AE，若AE平分∠DAB，∠EAC=25°，则∠AED的度数是______度．
【答案】85
【解析】
先证明∠B=∠EAD，然后利用SAS证明△ABC≌△EAD，得出∠AED=∠BAC．再证明△ABE为等边三角形，可得∠BAE=60°，求出∠BAC的度数，即可得∠AED的度数．
∵在平行四边形ABCD中，AD∥BC，BC=AD，∴∠EAD=∠AEB．
又∵AB=AE，∴∠B=∠AEB，∴∠B=∠EAD．在△ABC和△EAD中，∵AB=AE，∠ABC=∠EAD，BC=AD，∴△ABC≌△EAD（SAS），∴∠AED=∠BAC．
∵AE平分∠DAB，∴∠BAE=∠DAE，∴∠BAE=∠AEB=∠B，∴△ABE为等边三角形，∴∠BAE=60°，∴∠BAC=∠BAE+∠EAC=85°，∴∠AED=∠BAC=85°．
故答案为：85．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
【题目】为了更好的治理西流湖水质，保护环境，市治污公司决定购买 10 台污水处理设备．现有 A、B 两种型号的设备，其中每台的价格，月处理污水量如下表：
A 型 | B 型 | |
价格（万元/台） | a | b |
处理污水量（吨／月） | 240 | 200 |
经调查：购买一台 A 型设备比购买一台 B 型设备多 2 万元，购买 2 台 A 型设备比购买 3 台 B 型设备少 6 万元．
（1）求 a，b 的值；
（2）经预算：市治污公司购买污水处理设备的资金不超过 105 万元，你认为该公司 有哪几种购买方案；
（3）在（2）问的条件下，若每月要求处理西流湖的污水量不低于 2040 吨，为了节 约资金，请你为治污公司设计一种最省钱的购买方案．
