题目内容
【题目】如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH;
(2)若∠A=90°,求证:FG⊥FH;
(3)若∠A=80°,求∠GFH的度数.

【答案】(1)证明见解析;(2)证明见解析;(3)∠GFH=100°.
【解析】
(1)由中点性质及AB=AC,得到BD=EC,再由中位线性质证明FG∥BD,GF=![]() BD,FH∥EC,FH=
BD,FH∥EC,FH=![]() EC,从而得到FG=FH;
EC,从而得到FG=FH;
(2)由(1)FG∥BD,FH∥EC,再由∠A=90°,可证FG⊥FH;
(3)由(1)FG∥BD,∠A=80°,可求得∠FKC,再由FH∥EC,可求得∠GFH的度数.
(1)∵AB=AC,点D,E分别是边AB,AC的中点
∴BD=EC
∵点F,G,H分别为BE,DE,BC的中点
∴FG∥BD,GF=![]() BD
BD
FH∥EC,FH=![]() EC
EC
∴FG=FH;
(2)由(1)FG∥BD
又∵∠A=90°
∴FG⊥AC
∵FH∥EC
∴FG⊥FH;
(3)延长FG交AC于点K,
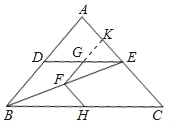
∵FG∥BD,∠A=80°
∴∠FKC=∠A=80°
∵FH∥EC
∴∠GFH=180°﹣∠FKC=100°

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目





