Question

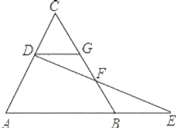
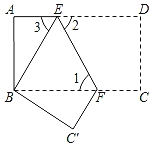
【题目】如图，把长方形纸片ABCD沿EF折叠后，使得点D与点B重合，点C落在点C′的位置上．

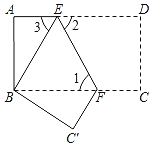
（1）折叠后，DC的对应线段是　 　，CF的对应线段是　 　．

（2）若∠1＝55°，求∠2、∠3的度数；

（3）若AB＝6，AD＝12，求△BC′F的面积．

Answer 1

【答案】（1）BC′， FC′；（2）∠2＝55°，∠3＝70°；（3）．

【解析】

(1)根据翻折性质即可解决问题.

(2)利用翻折的性质以及平行线的性质解决问题即可.

(3)根据ASA可证明△ABE≌△C′BF，求出△ABE的面积即可.

解：（1）折叠后，DC的对应线段是BC′，CF的对应线段是FC′．

故答案为BC′，FC′．

（2）由翻折的性质可知：∠2＝∠BEF，

∵AD∥BC，

∴∠2＝∠1＝55°，

∴∠3＝180°﹣2×55°＝70°．

（3）设DE＝EB＝x，

在Rt△ABE中，∵BE2＝AB2+AE2，

∴62+（12﹣x）2＝x2，

∴

∵∠ABC＝∠EBC′，

∴∠ABC-∠EBF＝∠EBC′-∠EBF

∴∠ABE＝∠FBC′，

在矩形ABCD中AB=CD

又∵BC′=CD

∴AB＝BC′

∵∠A＝∠C′＝90°

∴△ABE≌△C′BF（ASA），

∴S△BFC′＝S△ABE＝．