Question

【题目】如图，△ABC中，∠ACB＝90°，AC＝8cm，BC＝6cm．点P从A点出发沿A→C→B路径以每秒1cm的运动速度向终点B运动；同时点Q从B点出发沿B→C→A路径以每秒vcm的速度向终点A运动．分别过P和Q作PE⊥AB于E，QF⊥AB于F．

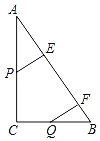
（1）设运动时间为t秒，当t＝　 　时，直线BP平分△ABC的面积．

（2）当Q在BC边上运动时（t＞0），且v＝1时，连接AQ、连接BP，线段AQ与BP可能相等吗？若能，求出t的值；若不能，请说明理由．

（3）当Q的速度v为多少时，存在某一时刻（或时间段）可以使得△PAE与△QBF全等．

Answer 1

【答案】（1）4；（2）当Q在BC边上运动时（t＞0），且v＝1时、线段AQ与BP不可能相等；（3）当v＝cm/s时．t＝时，△PAE与△QBF全等．

【解析】

(1)根据三角形的中线分三角形面积相等的两部分，可得当AP＝PC时，直线BP平分△ABC的面积由此即可解决问题.

(2) 假设可能相等，利用勾股定理构建方程即可解决问题.

(3)分两种情形: ①当点Q在线段BC上时，PA=BQ时，△AEP≌△FQB， ②当P，Q在AC边上相遇时，且PA=PB时, △PAE与△QBF全等.分别求解即可解决问题.

解：（1）当AP＝PC时，直线BP平分△ABC的面积．此时t＝4．

故答案为4．

（2）假设可能相等．则有82+（6﹣t）2＝62+（8﹣t）2，

解得t＝0，不符合题意，

所以当Q在BC边上运动时（t＞0），且v＝1时、线段AQ与BP不可能相等．

（3）①当点Q在线段BC上时，

在Rt△AEP和Rt△BFQ中，

∵∠AEP＝∠BFQ＝90°，∠C＝90°，

∴∠A+∠B＝90°，∠B+∠BQF＝90°，

∴∠A＝∠BQF，

∴当PA＝BQ时，△AEP≌△FQB，

∴当v＝1cm/s时，0＜t≤6时，△PAE与△QBF全等．

②当P，Q在AC边上相遇时，且PA＝PB时，△PAE与△QBF全等．设此时PA＝PB＝x，

在Rt△PBC中，∵PB2＝PC2+BC2，

∴x2＝（8﹣x）2+62，

∵当P，Q在AC边上相遇，可得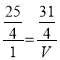

解得

∴当v＝cm/s时．t＝时，△PAE与△QBF全等．