题目内容
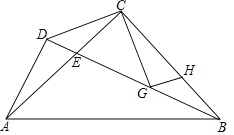
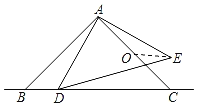
【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,则OE的最小值是为( )
A.![]() B.0.25C.1D.2
B.0.25C.1D.2
【答案】A
【解析】
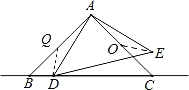
依题意设Q是AB的中点,连接DQ,先证得△AQD≌△AOE,得出QD=OE,根据点到直线的距离可知:当QD⊥BC时,QD最小,然后根据等腰直角三角形的性质求得QD⊥BC时的QD的值,即可求得线段OE的最小值.
解:设Q是AB的中点,连接DQ,
∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∵AB=AC=2,O为AC中点,
∴![]()
∴AQ=AO,
在△AQD和△AOE中,
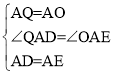 ,
,
∴△AQD≌△AOE(SAS),
∴QD=OE,
∵点D在直线BC上运动,
∴当QD⊥BC时,QD最小,
∵△ABC是等腰直角三角形,
∴∠B=45°,
∵QD⊥BC,
∴△QBD是等腰直角三角形,
∴![]()
∵QB=![]() AB=1,
AB=1,
∴![]()
∴线段OE的最小值是为![]() ;
;
故选:A.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
【题目】对于抛物线![]() .
.
(1)它与x轴交点的坐标为 ,与y轴交点的坐标为 ,顶点坐标为 ;
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |

(3)利用以上信息解答下列问题:若关于x的一元二次方程![]() (t为实数)在
(t为实数)在![]() <x<
<x<![]() 的范围内有解,则t的取值范围是 .
的范围内有解,则t的取值范围是 .