Question

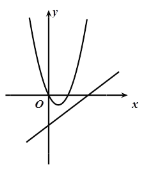
【题目】如图，在平面直角坐标系中，抛物线y＝ax2+bx+2（a≠0）与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，抛物线经过点D（﹣2，﹣3）和点E（3，2），点P是第一象限抛物线上的一个动点．

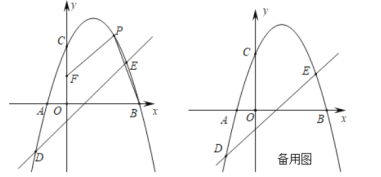
（1）求直线DE和抛物线的表达式；

（2）在y轴上取点F（0，1），连接PF，PB，当四边形OBPF的面积是7时，求点P的坐标；

（3）在（2）的条件下，当点P在抛物线对称轴的右侧时，直线DE上存在两点M，N（点M在点N的上方），且MN＝2，动点Q从点P出发，沿P→M→N→A的路线运动到终点A，当点Q的运动路程最短时，请直接写出此时点N的坐标．

Answer 1

【答案】（1）y＝x﹣1，y＝x2+x+2；（2）P（2，3）或（，）；（3）N（，）．

【解析】

（1）将点D、E的坐标代入函数表达式，即可求解；

（2）S四边形OBPF＝S△OBF+S△PFB＝×4×1+×PH×BO，即可求解；

（3）过点M作A′M∥AN，过作点A′直线DE的对称点A″，连接PA″交直线DE于点M，此时，点Q运动的路径最短，即可求解．

（1）将点D、E的坐标代入函数表达式得：，解得：

，故抛物线的表达式为：y＝x2+x+2，

同理可得直线DE的表达式为：y＝x﹣1…①；

（2）如图1，连接BF，过点P作PH∥y轴交BF于点H，

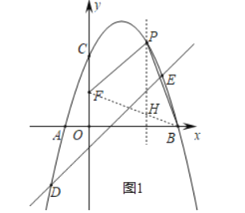
将点FB代入一次函数表达式，

同理可得直线BF的表达式为：y＝+1，

设点P（x，），则点H（x，+1），

S四边形OBPF＝S△OBF+S△PFB＝×4×1+×PH×BO＝2+2（）＝7，

解得：x＝2或，

故点P（2，3）或（，）；

（3）当点P在抛物线对称轴的右侧时，点P（2，3），

过点M作A′M∥AN，过作点A′直线DE的对称点A″，连接PA″交直线DE于点M，此时，点Q运动的路径最短，

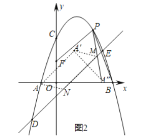
∵MN＝2，相当于向上、向右分别平移2个单位，故点A′（1，2），

A′A″⊥DE，则直线A′A″过点A′，则其表达式为：y＝﹣x+3…②，

联立①②得x＝2，则A′A″中点坐标为（2，1），

由中点坐标公式得：点A″（3，0），

同理可得：直线AP″的表达式为：y＝﹣3x+9…③，

联立①③并解得：x＝，即点M（，），

点M沿BD向下平移2个单位得：N（，）．