题目内容
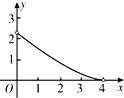
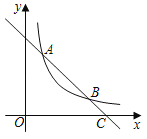
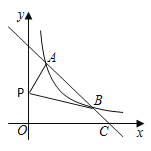
【题目】如图,一次函数y=﹣x+3的图象与反比例函数y=![]() (k≠0)在第一象限的图象交于A(1,a)和B两点,与x轴交于点C.
(k≠0)在第一象限的图象交于A(1,a)和B两点,与x轴交于点C.
(1)求反比例函数的解析式;
(2)若点P在x轴上,且△APC的面积为5,求点P的坐标;
(3)若点P在y轴上,是否存在点P,使△ABP是以AB为一直角边的直角三角形?若存在,求出所有符合条件的P点坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)(﹣2,0)或(8,0);(3)存在,P(0,1)或 P(0,﹣1)
;(2)(﹣2,0)或(8,0);(3)存在,P(0,1)或 P(0,﹣1)
【解析】
(1)将点A坐标代入两个解析式可求a的值,k的值,即可求解;
(2)设P(x,0),由三角形的面积公式可求解;
(3)分两种情况讨论,由两点距离公式分别求出AP,AB,BP的长,由勾股定理可求解.
(1)把点A(1,a)代入y=﹣x+3,得a=2,
∴A(1,2),
把A(1,2)代入反比例函数y=![]() ,
,
∴k=1×2=2;
∴反比例函数的表达式为![]() ;
;
(2)∵一次函数y=﹣x+3的图象与x轴交于点C,
∴C(3,0),
设P(x,0),
∴PC=|3﹣x|,
∴S△APC=![]() |3﹣x|×2=5,
|3﹣x|×2=5,
∴x=﹣2或x=8,
∴P的坐标为(﹣2,0)或(8,0);
(3)存在,
理由如下:联立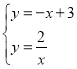 ,
,
解得:![]() 或
或![]() ,
,
∴B点坐标为(2,1),
∵点P在y轴上,
∴设P(0,m),
∴AB=![]() ,AP=
,AP=![]() ,PB=
,PB=![]() ,
,
若BP为斜边,
∴BP2=AB2+AP2 ,
即 ![]() =2+
=2+![]() ,
,
解得:m=1,
∴P(0,1);
若AP为斜边,
∴AP2=PB2+AB2 ,
即 ![]() =
=![]() +2,
+2,
解得:m=﹣1,
∴P(0,﹣1);
综上所述:P(0,1)或 P(0,﹣1).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目