题目内容
请你裁定,你一定要主持公道啊!
小明和小方分别设计了一种求n边形的内角和(n-2)×180°(n为大于2的整数)的方案:
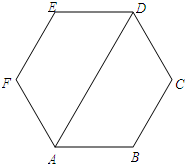
(1)小明是在n边形内取一点P,然后分别连结PA1、PA2、…、PAn(如图1);
(2)小红是在n边形的一边A1A2上任取一点P,然后分别连结PA4、PA5、…、PA1(如图2).
请你评判这两种方案是否可行?如果不行的话,请你说明理由;如果可行的话,请你沿着方案的设计思路把多边形的内角和求出来.

小明和小方分别设计了一种求n边形的内角和(n-2)×180°(n为大于2的整数)的方案:
(1)小明是在n边形内取一点P,然后分别连结PA1、PA2、…、PAn(如图1);
(2)小红是在n边形的一边A1A2上任取一点P,然后分别连结PA4、PA5、…、PA1(如图2).
请你评判这两种方案是否可行?如果不行的话,请你说明理由;如果可行的话,请你沿着方案的设计思路把多边形的内角和求出来.

这两种方案都是可行的:
方案一:如图1所示:n边形可分为n个三角形,
则多边形的内角和=n×180°-360°=(n-2)×180°;
方案二:如图2所示:n边形可分为(n-1)个三角形,
则多边形的内角和=(n-1)×180°-180°=(n-2)×180°;
方案一:如图1所示:n边形可分为n个三角形,
则多边形的内角和=n×180°-360°=(n-2)×180°;
方案二:如图2所示:n边形可分为(n-1)个三角形,
则多边形的内角和=(n-1)×180°-180°=(n-2)×180°;

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目