题目内容
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣4mx+n(m>0)与x轴交于A、B两点(点A在原点左侧),与y轴交于点C,且OB=2OA,连接AC、BC.
(1)求A、B两点的坐标;
(2)将线段AC绕点A旋转60°得到线段AC',若点C'在抛物线的对称轴上,求出此时抛物线的函数解析式.
【答案】(1)A(﹣4,0),B(8,0);(2)y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]()
【解析】
(1)设:OA=a,则OB=2a,抛物线的对称轴为x=2,则点A(-a,0)、B(2a,0),则x=2=![]() 求出a,即可求出A、B的坐标;
求出a,即可求出A、B的坐标;
(2)由题意得:CM=2,CH=4,OC=-n=N=AH,HM=6=GC′,线段AC绕点A旋转60°得到线段AC',则△ACC′为等边三角形,利用勾股定理,即可求解.
(1) 如图所示,设:OA=a,则OB=2a,抛物线的对称轴为x=![]() =2,
=2,
则点A(﹣a,0)、B(2a,0),
则x=2=![]() ,
,
解得:a=4
∴A(﹣4,0)、B(8,0)
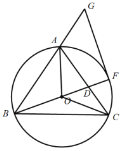
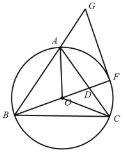
(2)过点A作y轴的平行线,分别交过点C、![]() 与x轴的平行线于点H、G,直线HC交对称轴于点M,则四边形
与x轴的平行线于点H、G,直线HC交对称轴于点M,则四边形![]() 为矩形,
为矩形,
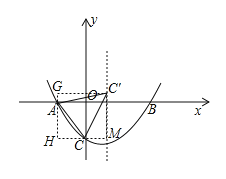
由题意得: CM=2, CH=4,OC=-n=N=AH, ![]() ,
,
线段AC绕点A旋转60°得到线段![]() ,则
,则![]() 为等边三角形,
为等边三角形,
则![]() ,
,
在![]() 中,
中,![]() ,
,
则![]() ,
,
在![]() 中,
中,![]() , 即:
, 即: ![]()
整理得:![]() ,
,
解得:![]() ,
,
即:![]()
∴y=mx2﹣4mx-![]()
把B(8,0)代入y=mx2﹣4mx-![]() 代入解得:
代入解得:![]()
故函数的表达式为:y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]()

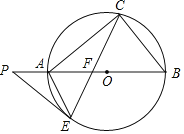
【题目】如图,AB 是⊙O 的弦,AB=5cm,点 P 是弦 AB 上的一个定点,点 C 是弧 AB 上的一 个动点,连接 CP 并延长,交⊙O 于点 D.
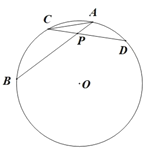
小明根据学习函数的经验,分别对 AC,PC,PD 长度之间的关系进行了探究.
下面是小明的探究过程:
(1)对于点 C 在弧 AB 上的不同位置,画图、测量,得到了线段 AC,PC,PD 的长度的 几组值,如下表:
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | 位置 9 | |
AC/cm | 0 | 0.37 | 1.00 | 1.82 | 2.10 | 3.00 | 3.50 | 3.91 | 5.00 |
PC/cm | 1.00 | 0.81 | 0.69 | 0.75 | 1.26 | 2.11 | 2.50 | 3.00 | 4.00 |
PD/cm | 4.00 | 5.00 | 5.80 | 6.00 | 3.00 | 1.90 | 1.50 | 1.32 | 1.00 |
在 AC,PC,PD 的长度这三个量中,确定___的长度是自变量,其他两条线段的长度都是这个自变量的函数;
(2)请你在同一平面直角坐标系 xOy 中, 画(1)中所确定的两个函数的图象;

(3)结合函数图象,解决问题:
①当 PC=PD 时,AC 的长度约为 cm;
②当△APC 为等腰三角形时,PC 的长度约为 cm.