题目内容
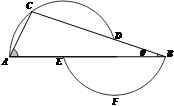
如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为弧EF的中点,BF交AD于点E,且BE·EF=32,AD=6.

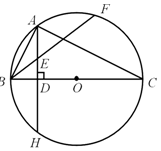
(1)求证:AE=BE;
(2)求DE的长;
(3)求BD的长 .


(1)求证:AE=BE;
(2)求DE的长;
(3)求BD的长 .
(1)连AF,由A为 的中点可得∠ABE=∠AFB,再根据圆周角定理可得∠AFB=∠ACB,即得∠ABE=∠ACB,由BC为直径可得∠BAC=90°,AH⊥BC,即可证得结论;(2)2;(3)
的中点可得∠ABE=∠AFB,再根据圆周角定理可得∠AFB=∠ACB,即得∠ABE=∠ACB,由BC为直径可得∠BAC=90°,AH⊥BC,即可证得结论;(2)2;(3)
 的中点可得∠ABE=∠AFB,再根据圆周角定理可得∠AFB=∠ACB,即得∠ABE=∠ACB,由BC为直径可得∠BAC=90°,AH⊥BC,即可证得结论;(2)2;(3)
的中点可得∠ABE=∠AFB,再根据圆周角定理可得∠AFB=∠ACB,即得∠ABE=∠ACB,由BC为直径可得∠BAC=90°,AH⊥BC,即可证得结论;(2)2;(3)
试题分析:(1)连AF,由A为
 的中点可得∠ABE=∠AFB,再根据圆周角定理可得∠AFB=∠ACB,即得∠ABE=∠ACB,由BC为直径可得∠BAC=90°,AH⊥BC,即可证得结论;
的中点可得∠ABE=∠AFB,再根据圆周角定理可得∠AFB=∠ACB,即得∠ABE=∠ACB,由BC为直径可得∠BAC=90°,AH⊥BC,即可证得结论;(2)设DE=x(x>0),由AD=6,BE•EF=32,AE•EH=BE•EF,可列式为(6-x)(6+x)=32,由此求解;
(3)由(1)、(2)有:BE=AE=6-2=4,根据Rt△BDE中的勾股定理求解.
(1)连AF,

∵A为
 的中点,
的中点,∴∠ABE=∠AFB,
又∠AFB=∠ACB,
∴∠ABE=∠ACB .
∵ BC为直径,
∴∠BAC=90°,AH⊥BC,
∴∠BAE=∠ACB,
∴∠ABE=∠BAE,
∴ AE=BE;
(2)设DE=x(x>0),由AD=6,BE·EF=32,AE·EH=BE·EF,
有(6-x)(6+x)=32,由此解得x=2, 即DE的长为2;
(3)由(1)、(2)有:BE=AE=6-2=4,
在RtΔBDE中,BD=
 =
= .
. 点评:圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,均等于所对圆心角的一半.

练习册系列答案
相关题目
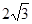 ,BD=2,则图中阴影部分的面积是 .
,BD=2,则图中阴影部分的面积是 .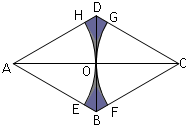
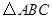 的顶点
的顶点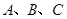 均在
均在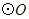 上,
上,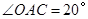 ,则
,则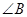 的度数为
的度数为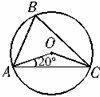
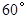
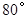
 交于
交于 、
、 两点,且与半径
两点,且与半径 垂直,垂足为
垂直,垂足为 ,
, ,在
,在 的延长线上取一点
的延长线上取一点 ,使得
,使得 .
.
 与
与 )
) 、
、 、
、 、
、 四点.已知
四点.已知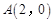 ,
,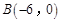 ,
,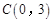 ,则点
,则点