题目内容
如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,P是BC上的动点,设PB=x,若能在AC上找到一点M,使∠BMP=90°,则x的取值范围是 。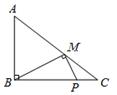

6≤x≤8
试题分析:根据已知首先找出BP取最小值时QO⊥AC,进而求出△ABC∽△OQC,再求出x的最小值,进而求出PB的取值范围即可.
过BP中点O,以BP为直径作圆,连接QO,当QO⊥AC时,QO最短,即BP最短
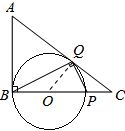
∵∠OQC=∠ABC=90°,∠C=∠C,
∴△ABC∽△OQC,
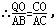
∵AB=6,BC=8,
∴AC=10,
∵BP=x,
∴QO=
 x,CO=8-
x,CO=8- x,
x,∴
 ,解得
,解得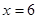
当P与C重合时,BP=8
∴BP=x的取值范围是:6≤x≤8.
点评:找出当QO⊥AC时,QO最短即BP最短,进而利用相似求出是解决问题的关键.

练习册系列答案
相关题目
 .
.

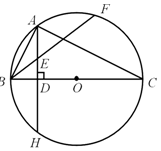

 的中点,过点D作直线BC的垂线,分别交CB、CA的延长线E、F
的中点,过点D作直线BC的垂线,分别交CB、CA的延长线E、F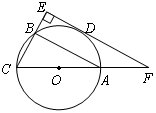
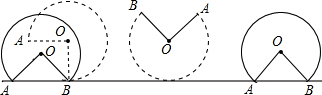
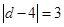 ,且两圆的半径是方程
,且两圆的半径是方程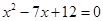 的两个根,试判断这两圆的位置关系.
的两个根,试判断这两圆的位置关系.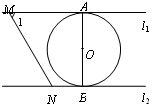
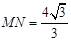 B.若MN与⊙O相切,则
B.若MN与⊙O相切,则