题目内容
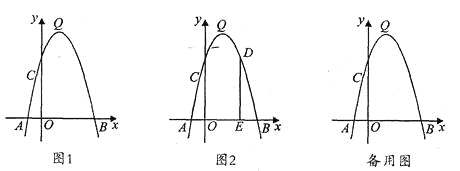
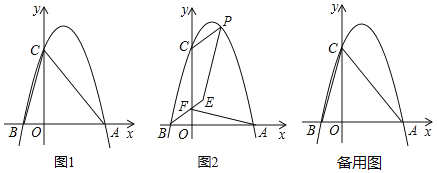
【题目】已知抛物线的解析式y=ax2+bx+3与x轴交于A、B两点,点B的坐标为(﹣1,0)抛物线与y轴正半轴交于点C,△ABC面积为6.
(1)如图1,求此抛物线的解析式;
(2)P为第一象限抛物线上一动点,过P作PG⊥AC,垂足为点G,设点P的横坐标为t,线段PG的长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;
(3)如图2,在(2)的条件下,过点B作CP的平行线交y轴上一点F,连接AF,在BF的延长线上取点E,连接PE,若PE=AF,∠AFE+∠BEP=180°,求点P的坐标.
【答案】(1)y=﹣x2+2x+3;(2)![]() ,0<t<3;(3)P(
,0<t<3;(3)P(![]() )
)
【解析】
(1)根据条件易求出A,B两点的坐标,再利用待定系数法求解即可;
(2)作PD⊥x轴交AC于点E,如图3,易知∠A=45°,然后利用三角形的内角和可得:∠P=∠A,则![]() ,再利用待定系数法求出直线AC的解析式,而点P的横坐标已知,则可用含t的代数式表示出PE,问题即得解决;
,再利用待定系数法求出直线AC的解析式,而点P的横坐标已知,则可用含t的代数式表示出PE,问题即得解决;
(3)如图4,过点P作PN⊥BE交BE于点N,过点C作CH⊥BE于点H,过点A作AG⊥BE于点G,设BE与AC交于点M,根据AAS可证明△PEN≌△AFG,可得PN=AG,然后再根据AAS证明△CHM≌△AGM,可得CM=AM,于是由中点坐标公式可求得点M的坐标,再根据待定系数法可求得直线BM的解析式,进而求出直线CP的解析式,然后解由直线CP和抛物线的解析式组成的方程组即可求出点P的坐标.
解:(1)当x=0时,y=3,∴C(0,3),∴OC=3,
∵B(﹣1,0),∴OB=1,∴![]() ,解得:AB=4,
,解得:AB=4,
∴OA=AB﹣OB=3,∴A(3,0),
将A,B的坐标代入抛物线的解析式y=ax2+bx+3,得:![]() ,解得;
,解得;![]() ,
,
∴抛物线的解析式为y=﹣x2+2x+3;
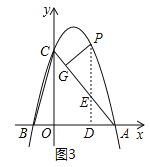
(2)作PD⊥x轴交AC于点E,如图3,
∵OA=OC=3,∴∠A=45°,
∵∠PEG=∠AED,∠PGE=∠EDA=90°,∴∠P=∠A=45°,
∴![]() ,∴
,∴![]() ,
,
设直线AC的解析式为:y=kx+b,把A(3,0),C(0,3)两点代入,得:![]() ,解得:
,解得:![]() ,
,
∴直线AC为y=﹣x+3,
设P(t,﹣t2+2t+3),∵PD⊥x轴,∴E(t,﹣t+3),
∴PE=﹣t2+2t+3+t﹣3=﹣t2+3t,∴![]() ,
,
∵P为第一象限抛物线上一动点,∴0<t<3;
∴![]() ,0<t<3;
,0<t<3;
(3)如图4,过点P作PN⊥BE交BE于点N,过点C作CH⊥BE于点H,过点A作AG⊥BE于点G,设BE与AC交于点M,
∵∠BEP+∠PEN=180°,∠AFE+∠BEP=180°,∴∠PEN=∠AFG,
∵∠PNE=∠AGF=90°,PE=AF,
∴△PEN≌△AFG(AAS),∴PN=AG,
∵CP∥BE,∴四边形CPNH是矩形,∴PN=CH=AG,
∵∠CMH=∠AMG,∠CHM=∠AGM,
∴△CHM≌△AGM(AAS),∴CM=AM,∴M(![]() ,
,![]() ),
),
则可得过点B(-1,0)和点M(![]() ,
,![]() )两点的直线解析式为:y=
)两点的直线解析式为:y=![]() ,
,
∵CP∥BM,∴直线CP的解析式为y=![]() ,
,
解方程组: ,得:
,得:![]() ,
,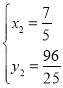 ,
,
∴P(![]() ).
).

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案